Question
Question: A \(10kg\) block is pulled along a frictionless surface in the form of an arc or a circle of radius ...
A 10kg block is pulled along a frictionless surface in the form of an arc or a circle of radius 10m The applied force is of 200N as shown in the figure. If the block started from rest at A, the velocity at B would be: (g=10ms−2)
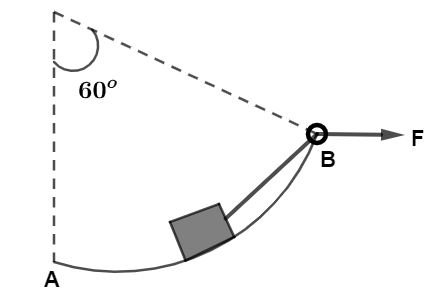
(A) 3ms−1
(B) 103ms−1
(C) 1003ms−1
(D) None of these
Solution
In order to solve this question, we will first find the work done by the applied force and the potential energy of block due to rise in height by drawing free body diagram and later will use the concept that work done will be equal to that of net energy used of the body.
Complete answer:
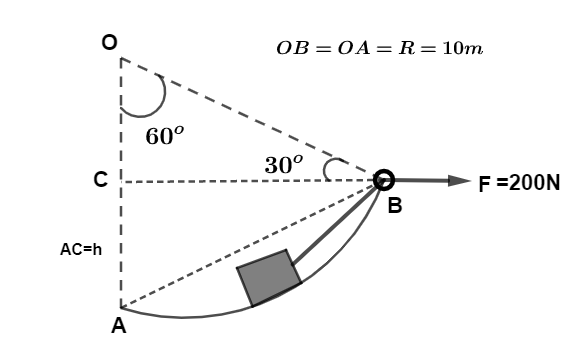
Let us first draw the diagram as:
OA=OB=R=10m radius if circular arc given in question.
Let AC be the height from point A to which block is raised to reach point B.
Since, In ΔOAB OA=OB so remaining angles ∠OAB=∠OBA=600 which makes triangle OAB a equilateral triangle such that distance covered by the block due to applied force F=200N will be AB=OA=R=10m hence, work done by the force is given by,
W=F.AB
on putting the values we get,
W=2000J→(i)
Now, mass of the block is given by m=10kg
acceleration due to gravity is g=10ms−2
and height to which block is raised is AC=h
now, in right angle triangle OCB we have,
sin300=OBOC we know sin300=21,OB=R=10m on putting these values we get,
21=10OC
⇒OC=5m now the height h can be written as from diagram we have,
AC=OA−OC
AC=h=10−5=5m
so height is given by h=5m
hence, potential energy of the block is
P.E=mgh on putting the values we get,
P.E=10×10×5
⇒P.E=500J→(ii)
Now, the kinetic energy of the block while it’s at rest at point A is K.EA=0
Let K.E of the block at point B with velocity v is K.EB=21mv2→(iii)
Now, Sum of all energy of the block will be equal to work done by the applied force so, net energy on the block is sum of potential energy and change in Kinetic energy so,
W=P.E+K.EB−K.EA
on putting the values of these parameters from equation (i) , (ii) and (ii) we get,
2000=500+21×10×v2−0
2000−500=5v2
1500=5v2
⇒v=300
⇒v=103ms−1
Hence, the correct option is (B) 103ms−1.
Note: It should be remembered that, the work done by a body is equal to change in energy of a body is referred as Work Energy theorem. and also when two sides of a triangle are equal then the opposite angles of these sides are also equal is an property of triangles. In an equilateral triangle all sides are equal and all angles are of 600 each.
