Question

A $100cm$ long cylindrical flask with inner and outer radius ${r_1} = 2cm$ and ${r_2} = 4cm$ respectively, is completely filled with ice at as shown in the figure.

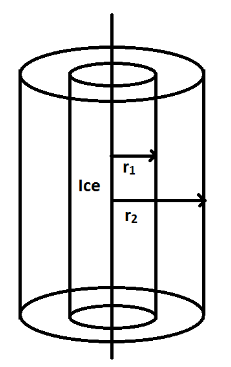
The constant temperature outside (surrounding) the flask is. Assume heat exchange occurs only through the curved surface of the flask. (Thermal conductivity of the flask is, ${L_{ice}} = 80cal/gm$ and$1cal = 4200J$).
A. Rate of heat flow from surrounding to the flask is $80\pi J/s$
B. The rate at which ice melts is $\dfrac{\pi }{{4200}}kg/s$
C. The rate at which ice melts is $100\pi kg/s$
D. Rate of heat flow from surrounding to the flask is $40\pi J/s$

Answer 1

In this question, we need to find two things, the rate at which the ice melts and the heat flow from the surroundings to the flask. To solve this, we will use two formulas. First the formula for thermal conductivity which will give us the rate of heat flow from surrounding to the flask. After that, we will use the formula for latent heat to determine the rate at which the ice melts.

Formulas used:
$K = \dfrac{{Qdr}}{{Ad\theta }}$
where, $K$ is the thermal conductivity, $Q$ is the amount of heat transferred through the material, $dr$ is the distance between two isothermal planes, $A$ is the area of the surface and$d\theta$ is the difference in the temperature.
$Q = \dfrac{{dm}}{{dt}}L$
where, $Q$ is the amount of heat transferred through the material, $\dfrac{{dm}}{{dt}}$ is the rate of melting of ice and $L$ is the latent heat of the material

Complete step by step answer:
First, we will find the rate at which the ice melts. This is nothing but Rate of heat flow from surrounding to the flask .We know that

K = \dfrac{{Qdr}}{{Ad\theta }} \\\ \Rightarrow Qdr = KAd\theta \\\ $$ We know that the surface area of the cylinder is given by $A = 2\pi rl$

\Rightarrow Qdr = K\left( {2\pi rl} \right)d\theta \\
\Rightarrow Q\dfrac{{dr}}{r} = 2\pi Kld\theta \\ $$
We will now integrate both sides

$$\Rightarrow Q\int\limits_{{r_1}}^{{r_2}} {\dfrac{{dr}}{r}} = 2\pi Kl\int\limits_{{\theta _1}}^{{\theta _2}} {d\theta } \\\ \Rightarrow Q\left( {\ln {r_2} - \ln {r_1}} \right) = 2\pi Kl\left( {{\theta _2} - {\theta _1}} \right) \\\ \Rightarrow Q\ln \dfrac{{{r_2}}}{{{r_1}}} = 2\pi Kl\left( {{\theta _2} - {\theta _1}} \right) \\\$$

We are given ${r_1} = 2cm = 0.02m$, ${r_2} = 4cm = 0.04m$, and $l = 100cm = 1m$

\Rightarrow Q\ln \dfrac{{0.04}}{{0.02}} = 2\pi \times 0.693 \times 1 \times \left( {40 - 0} \right) \\\ \Rightarrow Q\ln 2 = 2\pi \times 0.693 \times 1 \times 40 \\\ \Rightarrow Q \times 0.693 = 2\pi \times 0.693 \times 1 \times 40 \\\ \Rightarrow Q = 80\pi J/s \\\ $$ Thus, the rate of heat flow from surrounding to the flask is $$80\pi J/s$$. Hence, option A is the right answer. Now, we will find the rate at which the ice melts. $Q = \dfrac{{dm}}{{dt}}L$ We have $$Q = 80\pi J/s$$ and $${L_{ice}} = 80cal/gm = 4200 \times 80J$$ $\dfrac{{dm}}{{dt}} = \dfrac{Q}{{{L_{ice}}}} \\\ \Rightarrow\dfrac{{dm}}{{dt}} = \dfrac{{80\pi }}{{80 \times 4200}} \\\ \therefore\dfrac{{dm}}{{dt}} = \dfrac{\pi }{{4200}}kg/s$ Thus, The rate at which ice melts is $$\dfrac{\pi }{{4200}}kg/s$$. Hence, option B is also the right answer. **Therefore, option A and option B both are correct answers.** **Note:** To solve this question, we have used the concepts of thermal conductivity and latent heat. Thermal conductivity is defined as the ability of a given material to conduct or transfer the heat. The latent heat is defined as the heat required to convert a solid into a liquid or vapour, or a liquid into a vapour, without change of temperature.