Question

A $100{\text{m}}$ long train crosses a man travelling at $5{\text{km}}{{\text{h}}^{ - 1}}$ in the opposite direction in $7 \cdot 2{\text{s}}$. Find the velocity of the train.
A) ${\text{40km}}{{\text{h}}^{ - 1}}$
B) $25{\text{km}}{{\text{h}}^{ - 1}}$
C) ${\text{20km}}{{\text{h}}^{ - 1}}$
D) $45{\text{km}}{{\text{h}}^{ - 1}}$

Answer 1

Here both the train and the man are moving with some velocity. So we consider the relative velocity of the train with respect to that of the man. Here the distance covered by the train as it crosses the man will be the length of the train.

Formulas used:
-The relative velocity of body A with respect to body B is given by, ${v_{A/B}} = {v_A} - {v_B}$ where ${v_A}$ and ${v_B}$ are the velocities of the body A and body B respectively.
-The velocity of a body is given by, $v = \dfrac{d}{t}$ where $d$ is the displacement of the body and $t$ is the time taken.

Complete step by step answer.
Step 1: Sketch a figure depicting the given scenario.

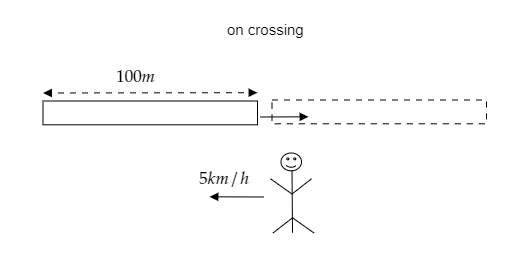
As seen from the figure, the distance covered or the displacement of the train as it crosses the man moving towards it will be equal to the length of the train.
i.e., if $d$ is the displacement of the train and $l = 100{\text{m}}$ is the length of the train, then we have $d = l = 100{\text{m}}$ .
The time taken for the train to cross the man is given to be $t = 7 \cdot 2{\text{s}}$ .
The velocity of the man is given to be ${v_M} = 5{\text{km}}{{\text{h}}^{ - 1}}$.
Let ${v_{T/M}}$ be the relative velocity of the train and ${v_T}$ be the actual velocity of the train which is to be determined.
Step 2: Express the velocity of the train with respect to the man.
The relative velocity of the train can be expressed as ${v_{T/M}} = {v_T} - {v_M}$ -------- (1)
Substituting for ${v_M} = - 5{\text{km}}{{\text{h}}^{ - 1}}$ in equation (1) we get, ${v_{T/M}} = {v_T} + 5$
Thus the relative velocity of the train is ${v_{T/M}} = {v_T} + 5$ .
This relative velocity of the train can also be expressed as ${v_{T/M}} = \dfrac{d}{t}$ --------- (2)
Substituting for ${v_{T/M}} = {v_T} + 5$, $d = 0 \cdot 1{\text{m}}$ and $t = \dfrac{{7 \cdot 2}}{{3600}}{\text{h}}$ in equation (2) we get, ${v_T} + 5 = \dfrac{{0 \cdot 1}}{{7 \cdot 2}} \times 3600$
$\Rightarrow {v_T} = \dfrac{{0 \cdot 1 \times 3600}}{{7 \cdot 2}} - 5 = 45{\text{km}}{{\text{h}}^{ - 1}}$
Thus the velocity of the train is ${v_T} = 45{\text{km}}{{\text{h}}^{ - 1}}$ .

So the correct option is D.

Note: Here the man is moving in a direction opposite to the motion of the train. We assumed the man to be moving along the negative x-direction and the train to be moving along the positive x-direction. So we substitute ${v_M} = - 5{\text{km}}{{\text{h}}^{ - 1}}$ in equation (1). Here for convenience, the distance is converted to be in kilometres and time is converted to be in hours while substituting in equation (2) so that the velocity is obtained in ${\text{km}}{{\text{h}}^{ - 1}}$ .