Question
Question: A 10 Volts battery of internal resistance one ohm is connected to a 20 Volts battery of internal res...
A 10 Volts battery of internal resistance one ohm is connected to a 20 Volts battery of internal resistance 2 ohm. The combination is put across a resistance of 30 ohm. Find the current through each battery.
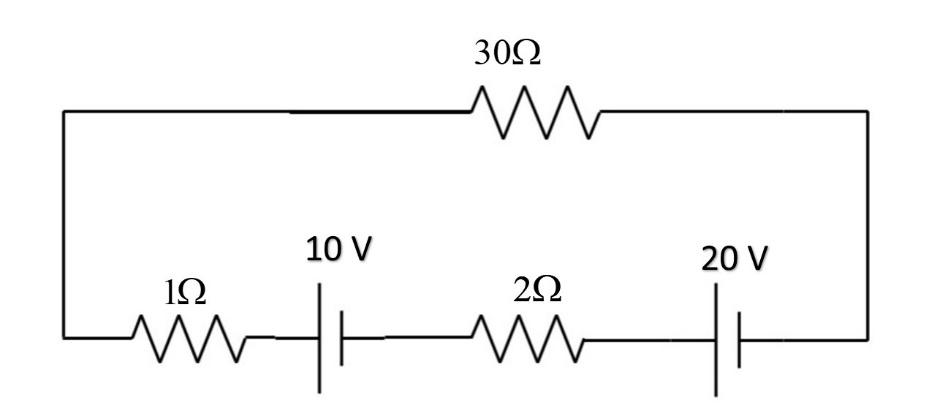
Solution
When the batteries are connected in series, we can assume the algebraic sum of voltages of all the batteries as the voltage of a single battery which can be connected in the circuit to produce the same potential difference as all collectively are producing.
Formula used: Ohm’s law: V=IR
Complete step by step answer:
We can replace the combination of different batteries as a single battery with a voltage given by the sum of voltages of individual batteries.
Hence Vnet=V1+V2
⟹Vnet=10+20=30V
Also, when resistors are connected in series, the net resistance of the circuit is given by the algebraic sum of individual resistances. Hence the total resistance of the circuit is given by;
Rnet=R1+R2+R3+...
⟹Rnet=30+1+2=33Ω
Now, using ohm’s law:
V=IR
⟹I=RV
⟹I=3330=1110A
Now, in series circuit, the current is the same for all circuital elements. Hence the current through both the batteries is same as 1110A
Additional information:
Practically, every battery has its own internal resistance. This is the same as any other external resistance and hence can be treated as a separate resistor in the circuit, placed next to the battery. In series circuit, the concept is simple and straight but for parallel combination, we have to use Kirchhoff’s law to find the result.
Note:
Chance of mistake is that one might think that the voltage of the battery is 20V and resistance 2 Ω, thus using ohm’s law, current is 10 A. This is completely wrong because we have to consider the load of all the resistors present in the circuit. This could be true only when there is no external resistance in the circuit.
