Question

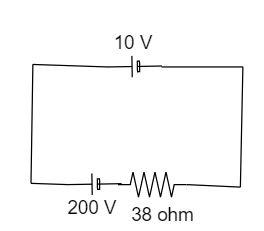
A 10 V cell of negligible internal resistance is connected in parallel across a battery of emf $200\,V$ and internal resistance $38\,\Omega$ as shown in the figure. Find the value of current in the circuit.

Answer 1

Find the value of the total net electro motive force by subtracting the value of the negligible resistance from the total emf of the battery. Substitute the obtained emf value in the rearranged ohm’s formula to find the value of the current flowing through the circuit.

Useful formula:
The ohm’s law is given by
$V = IR$
Where $V$ is the potential difference if the emf across the circuit, $I$ is the current in the circuit and the $R$ is the resistance in the circuit.

Complete step by step solution:
It is given that the
Internal resistance of the circuit, $r = 10\,V$
The emf across the battery, ${r_e} = 200\,V$
The net resistance of the circuit, $R = 38\,\Omega$
The net emf in the circuit is calculated by subtracting the negligible internal resistance from the total emf of the circuit.
$E = {r_e} - r$
Substituting the values in the above equation
$E = 200 - 10$
Subtracting the values in the right hand side.
$E = 190\,V$
Substituting the value of the emf in the ohm’s law.
$V = IR$
By rearranging the above formula,
$I = \dfrac{V}{R}$
Substituting the values of the resistance in the emf in the above step.
$I = \dfrac{{190}}{{38}}$
By doing the simple division in the above step.
$I = 5\,A$

The value of the current in the given circuit is $5\,A$.

Note: The electromotive force is the energy per unit charge that is produced from either battery or the generator. In the battery, the energy is converted from one form to the other. The internal resistance in the battery itself, because of the heating of its own parts.