Question

A 10 kg boy standing in a 40 kg boat floating on water is 20 meters from the shore of the river. If he moves 8 meters on the boat towards the shore, then how far is he from the shore now?

Answer 1

In this question, we need to determine the distance of the boy from the shore when he moved towards the shore by 8 meters. For this, we will follow the concept of momentum.

Complete step by step answer: Let the boy was standing at the farthest end of the boat. As the boat was in the water so, when the boy towards the shore (by 8 meters) then, the boat will also move in the opposite direction of the movement of the boy, i.e., away from the shore.
The following figure depicts the pictorial representation of the scenario.

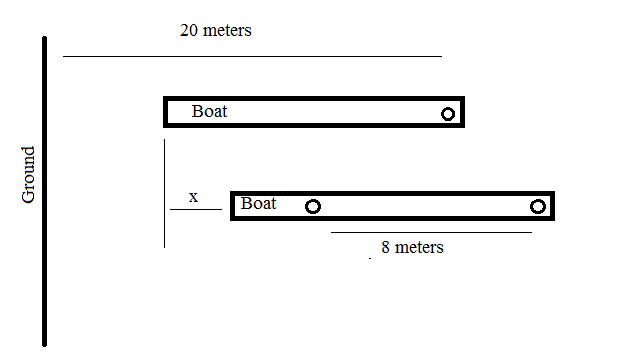
Let the boat moves back by $x$ meters away from the shore.
As the system was at rest initially, so the momentum of the whole system will remain constant. Moreover, there is no additional mass on the boat so the momentum will remain the same.
The product of the mass and the displacement of the body results in the momentum of the body. Mathematically, $M = mr$.
Substitute mass of the boat as 40 kg and the displacement as x meters in the equation $M = mr$.
Here, the momentum of the boat is given as ${m_1}{r_1} = 40x - - - - (i)$
The displacement of the boy with respect to the boat is given as $(8 - x)$ meters.
So, substitute mass of the boy as 10 kg and the displacement of the boy as (8-x) meters in the equation $M = mr$.
Here, the momentum of the boy is given as
${m_2}{r_2} = 10 \times \left( {8 - x} \right) \\\ = 80 - 10x \\\$
As the momentum is conserved here so,
${m_1}{r_1} = {m_2}{r_2} \\\ 40x = 80 - 10x \\\ 50x = 80 \\\ x = \dfrac{8}{5} \\\ = 1.6{\text{ meters}} \\\$
Now, the distance of the boy from the shore is given as
$d = 20 - \left( {8 - x} \right) \\\ = 20 - 8 + 1.6 \\\ = 13.6{\text{ meters}} \\\$
Hence, the distance of the boy from the shore is 13.6 meters.

Note: It is interesting to note here that as the boy moves towards the shore then he pushes the boat with his feet away from the shore and so, the boat moves backward.