Question
Question: A 10 D lens is used as a magnifier. The distance where the object should be placed to obtain maximum...
A 10 D lens is used as a magnifier. The distance where the object should be placed to obtain maximum angular magnification for a normal eye (near point 25 cm) is
Solution
We are given the power of a lens which is used as a magnifier. We know that when we obtain maximum angular magnification, the image will be formed at the near point of the eye. By obtaining focal length from power and substituting the known values in the lens formula, we will get the solution.
Formula used:
Power of a lens, P=f1
Lens formula, f1=v1−u1
Complete answer:
In the question we are given the power of a lens and it is said the lens is used as a magnifier.
We know that when we obtain maximum angular magnification, the image will be formed at the near point of eye.
Here the near point is given as 25 cm.
Since the image is formed at near point, we can write that
v=−25cm
The power of the lens is given as 10 D, i.e.
P=10D
We know that power,
P=f1, were ‘f’ is the focal length of the lens.
By substituting the given value of power in the above equation, we get
⇒10=f1
⇒f=101m
By converting to centimeter, we get
⇒f=10100cm
⇒f=10cm
Now let us apply the lens formula.
According to lens formula we know that,
f1=v1−u1, were ‘f’ is the focal length, ‘v’ is the image distance and ‘u’ is the object distance.
From earlier calculations we know the value of focal length and image distance. By substituting them in the lens formula, we get
⇒101=−251−u1
⇒101+251=−u1
From the above equation, we can solve for ‘u’.
⇒−u1=25035=507
⇒u1=−507
⇒u=−750
⇒u=−7.14cm
Hence the object should be kept at –7.14 cm distance to obtain maximum angular magnification for a normal eye.
Note:
Consider the figure of the convex mirror given below.
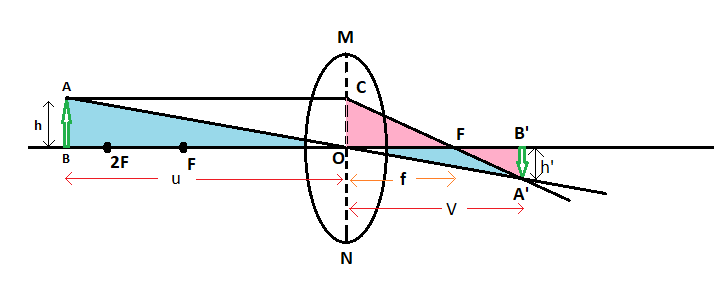
In the figure AB is the object and A’B’ is the image.
‘u’ is the object distance, ‘v’ is the image distance, ‘f’ is the focal length, ‘h’ is the length of the object and ‘h’’ is the length of the image.
Let ‘O’ be the optical centre of the lens, ‘F’ be the principal focus.
Now let us consider the triangle ABO and triangle A’B’O.
We can see that these two triangles are similar.
Therefore,
ABA′B′=OBOB′
Similarly we can see that triangle A’B’F and triangle OCF are similar.
Therefore,
OCA′B′=OFFB′
But we know that OC=AB
Therefore we get,
ABA′B′=OFFB′
Now we have,
ABA′B′=OBOB′ and ABA′B′=OFFB′
Since the left hand sides of both these equations are the same, we can equate the right hand side. Thus we get,
OBOB′=OFFB′
From the figure we can see that FB′=OB′−OF. By substituting this in the above equation, we get
OBOB′=OFOB′−OF
We know that
OB=−u
OB′=v
OF=f
Now let us substitute this, thus we get
−uv=fv−f
⇒vf=−uv+uf
⇒uv=uf−vf
Now let us divide the whole equation with uvf
Therefore,
⇒uvfuv=uvfuf−uvfvf
By simplifying this we get,
⇒f1=v1−u1
This is known as the lens formula.
