Question: A 1 cm height needle is placed at a distance of 0.1 m from a convex mirror of focal length 0.05 m, t...

Question

A 1 cm height needle is placed at a distance of 0.1 m from a convex mirror of focal length 0.05 m, then size of the image is
A. 1 cm
B. 0.66 cm
C. 0.33 cm
D. 0.5 cm

Answer 1

Solution

In case of mirrors usually there are three types used. Plain mirror, concave mirror and convex mirror. All will serve different purposes. Properties of different mirrors are different. In case of convex mirrors they always form virtual images. Images are always erect and diminished.
Formula used:
$m = \dfrac{{ - v}}{u} = \dfrac{f}{{f - u}} = \dfrac{{{h_i}}}{{{h_o}}}$

Complete answer:
Various positions of placing an object in front of a convex mirror gives us a virtual diminished image at various positions of the other side of the mirror.
If an object is placed between the pole and focus of the convex mirror then image will be formed on the other side of the mirror. That image formed will be diminished and virtual
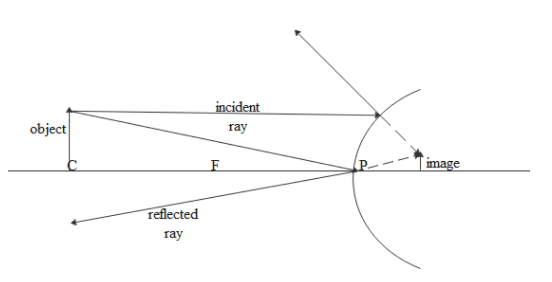
Now if we place an object between focus and center or at the center then the image is formed on the other side of the mirror and the image will be virtual and diminished. The size of the image will be smaller than an object as shown in the diagram.

Magnification is given as
$m = \dfrac{{ - v}}{u} = \dfrac{f}{{f - u}}$ where ‘v’ is the image distance and ‘u’ is the object distance and ‘f’ is the focal length.
In the given question $u = - 0.1m,f = + 0.05m$
From this we get magnification as
$m = \dfrac{f}{{f - u}}$
$\eqalign{ & \Rightarrow m = \dfrac{{0.05}}{{0.15}} \cr & \Rightarrow m = 0.33 \cr}$
We have height of object as 1 centimeter
$m = \dfrac{{{h_i}}}{{{h_o}}}$
Where ${h_i}$ is the height of the image and ${h_o}$ is the height of the object.
$m = \dfrac{{{h_i}}}{{{h_o}}}$
$\eqalign{ & \Rightarrow 0.33 = \dfrac{{{h_i}}}{{1cm}} \cr & \Rightarrow {h_i} = 0.33cm \cr}$

Hence option C will be the correct answer.

Note:
The image formed in case of a convex mirror is not a real image, that means it cannot be caught on the screen. The reflecting rays will be diverging and we have to extend those rays backwards to get the height and the position of the image.