Question

A $1.2m$ tall girl spots a balloon moving with the wind in a horizontal line at a height of $88.2m$ from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is $60^\circ$. After some time, the angle of elevation reduces to $30^\circ$. Find the distance travelled by the balloon during the interval.
A.$17\sqrt 2 m$
B.$34m$
C.$58\sqrt 3 m$
D.$67m$

Answer 1

Hint- In this question, we will consider $\vartriangle ACE$ and $\vartriangle BCG$ and apply tangent of angles in these triangles to calculate $CE$ and $CG$ to calculate $EG$ which is the required distance travelled by the balloon.

Complete step-by-step answer:

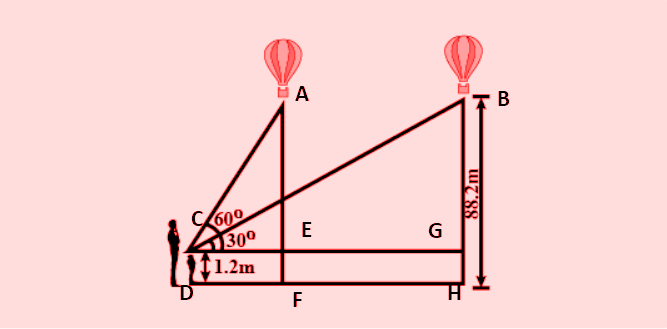
According to question,
We need to calculate the distance travelled by balloon that is from E to G,
So, considering $\vartriangle ACE$,
$\Rightarrow \dfrac{{AE}}{{CE}} = \tan 60^\circ$
$\Rightarrow \dfrac{{88.2 - 1.2}}{{CE}} = \sqrt 3$
$\Rightarrow CE = 29\sqrt 3 m$ …(1)
Considering $\vartriangle BCG$,
$\Rightarrow \dfrac{{BG}}{{CG}} = \tan 30^\circ$
$\Rightarrow \dfrac{{88.2 - 1.2}}{{CG}} = \dfrac{1}{{\sqrt 3 }}$
$\Rightarrow CG = 87\sqrt 3 m$ …(2)
We have to calculate $EG$ which is the distance travelled by the balloon,
$\Rightarrow EG = CG - CE$
$\Rightarrow EG = 87\sqrt 3 - 29\sqrt 3$
$\Rightarrow EG = 58\sqrt 3 m$
Hence, we obtain the distance travelled by the balloon equal to $58\sqrt 3 m$. So, option (C) is correct.
Note- For solving any question based on height and distance, the first and foremost thing is the diagram. So, we should make the diagram first and label it according to the question. Our next step should be to find the angle and triangle which are important with respect to the unknown in the question, and then apply sine, cosine, tangent in triangles to obtain the result as required.