Question

A $1.05m$ having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Fig. The cross-sectional areas of wires A and B are$1.0m{{m}^{2}}$ and $2.0m{{m}^{2}}$ respectively. At what point along the rod should a mass $m$ be suspended in order to produce
(a) Equal stress in A and B and
(b) Equal strains in A and B?

Answer 1

First consider the mass is suspended at a distance $l$ from the end where A is attached. Then calculate the stress on the rod. For equal stress the torque should be equal so by equating the torque you can calculate the value of $l$. Similarly for equal strain the torques must be equal. By equating the torque the length lengthy at which the mass should be attached can be calculated.
Formulas used:
$\text{Stress}=\dfrac{\text{Force}}{\text{Cross-sectional area}}=\dfrac{F}{A}$
$\tau =Fl$
Where symbols carry their usual meaning.

Complete answer:
Given that the cross-sectional area of rod A is ${{A}_{1}}=1.0m{{m}^{2}}=1.0\times {{10}^{-6}}{{m}^{2}}$
The cross-sectional area of rod B is ${{A}_{2}}=2.0m{{m}^{2}}=2.0\times {{10}^{-6}}{{m}^{2}}$
The known value of Young’s modulus for steel is,${{Y}_{1}}=2\times {{10}^{11}}N{{m}^{-2}}$ and
The known value of Young’s modulus for aluminium is,${{Y}_{2}}=7\times {{10}^{10}}N{{m}^{-2}}$

Case I: Equal stress in A and B:

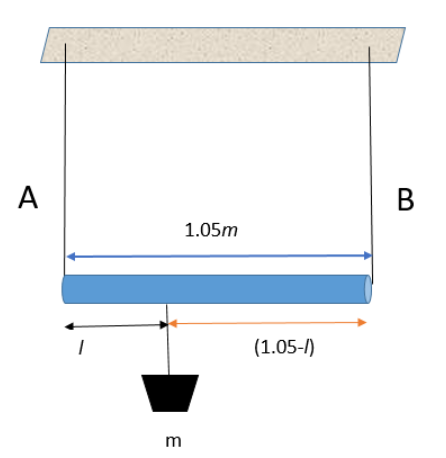
Consider a block of mass $m$is suspended on the rod at a distance $l$ from the end A.
The stress on the wire is given by the force per unit cross-sectional area. So
Stress on the wire due to mass $m$ is $\text{Stress}=\dfrac{\text{Force}}{\text{Cross-sectional area}}=\dfrac{F}{A}$
For the two wires(A and B) to have equal stresses, then
$\begin{aligned} & \text{Stress on A=Stress on B} \\\ & \dfrac{{{F}_{1}}}{{{A}_{1}}}=\dfrac{{{F}_{2}}}{{{A}_{2}}} \\\ \end{aligned}$
Where

& {{F}_{1}}=\text{ Stress Exerted on the steel wire } \\\ & {{F}_{2}}=\text{ Stress Exerted on the Aluminium wire } \\\ \end{aligned}$$ Then $\dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{{{A}_{1}}}{{{A}_{2}}}=\dfrac{1.0\times {{10}^{-6}}}{2.0\times {{10}^{-6}}}=\dfrac{1}{2}$ Torque about the point of the suspension is given by the product of force and distance of Force from the mass. So let the torque on the rod from the point of suspension about the wire A is ${{\tau }_{1}}$ and the torque on the rod from the point of suspension about the wire B${{\tau }_{2}}$. so $${{\tau }_{1}}={{F}_{1}}l$$ and $${{\tau }_{2}}={{F}_{2}}\left( 1.05-l \right)$$. For equal stresses the torques must be equal. So $$\begin{aligned} & {{\tau }_{1}}={{\tau }_{2}} \\\ & \Rightarrow {{F}_{1}}l={{F}_{2}}\left( 1.05-l \right) \\\ & \Rightarrow \dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{\left( 1.05-l \right)}{l} \\\ \end{aligned}$$ But$$\dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{1}{2}$$, so $$\begin{aligned} & \dfrac{\left( 1.05-l \right)}{l}=\dfrac{1}{2} \\\ & \Rightarrow 2\left( 1.05-l \right)=l \\\ & \Rightarrow 2.1-2l=l \\\ & \Rightarrow l=\dfrac{2.1}{3}=0.7m \\\ \end{aligned}$$ So the block should be attached at a distance $0.7m$ from the end where the wire A is attached in order to produce equal stress on the two wires. **Case II: Equal strains in A and B.**  Strain measures the capability of an object to undergo deformation when a deforming force is applied. The Young’s modulus of an object is defined as the ratio of stress to strain. So, $\begin{aligned} & \text{Young }\\!\\!'\\!\\!\text{ s Modulus=}\dfrac{\text{Stress}}{\text{Strain}} \\\ & \text{Strain=}\dfrac{\text{Stress}}{\text{Young }\\!\\!'\\!\\!\text{ s Modulus}}=\dfrac{\left( \dfrac{F}{A} \right)}{Y}=\dfrac{F}{AY} \\\ \end{aligned}$ For the strain on two wire to be equal i.e. strain on wire A will be equal to Strain on wire B then $\begin{aligned} & \dfrac{{{F}_{1}}}{{{A}_{1}}{{Y}_{1}}}=\dfrac{{{F}_{2}}}{{{A}_{2}}{{Y}_{2}}} \\\ & \Rightarrow \dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{{{A}_{1}}{{Y}_{1}}}{{{A}_{2}}{{Y}_{2}}}=\dfrac{1.0\times {{10}^{-6}}\times 2\times {{10}^{11}}}{2.0\times {{10}^{-6}}\times 7\times {{10}^{10}}}=\dfrac{10}{7} \\\ \end{aligned}$ Let a block of mass $m$ be suspended on the rod at a distance $l'$ from the end where the wire A is attached to the rod. For equal strain The torque about the point where mass is suspended must be equal. So $\begin{aligned} & {{F}_{1}}{l}'={{F}_{2}}\left( 1.05-l' \right) \\\ & \Rightarrow \dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{\left( 1.05-l' \right)}{l'} \\\ \end{aligned}$ But $\dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{10}{7}$, so $\begin{aligned} & \dfrac{\left( 1.05-l' \right)}{l'}=\dfrac{10}{7} \\\ & \Rightarrow 7.35-7l'=10l' \\\ & \Rightarrow 17l'=7.35 \\\ & \Rightarrow l'=\dfrac{7.35}{17}=0.432m \\\ \end{aligned}$ So the block should be attached at a distance $0.432m$ from the end where the wire A is attached in order to produce equal strain on the two wires. **Note:** Note that strain is the effect of stress. If there is no stress then the body will not undergo deformation and the strain will be zero. So to produce strain the stress or deforming force is necessary.