Solveeit Logo
Login

Question

Question: The equation of line equally inclined to co-ordinate axes and passing through $(-3, 2, -5)$...

The equation of line equally inclined to co-ordinate axes and passing through (−3,2,−5)(-3, 2, -5)

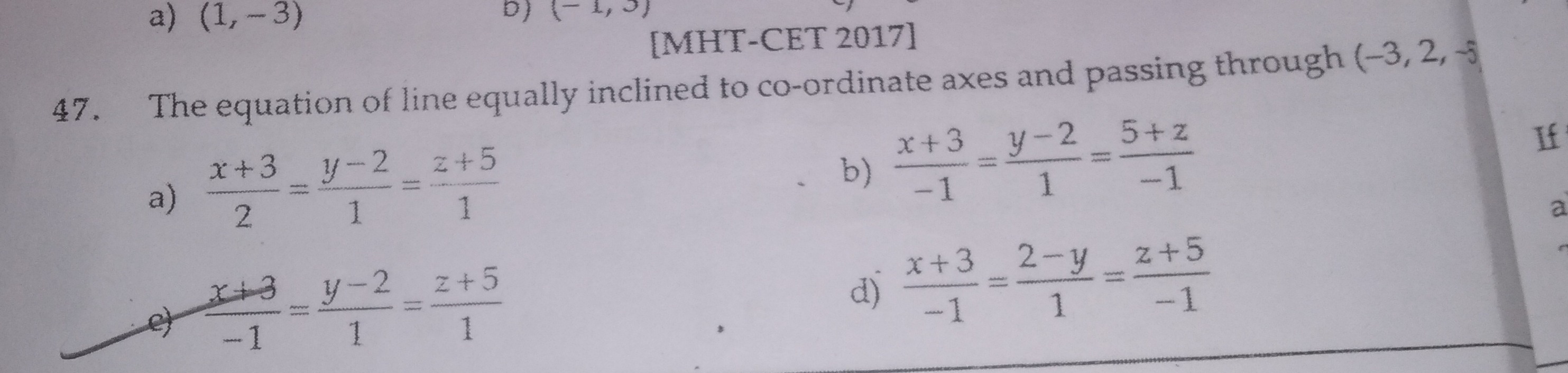
A

x+32=y−21=z+51\frac{x+3}{2}=\frac{y-2}{1}=\frac{z+5}{1}

B

x+3−1=y−21=5+z−1\frac{x+3}{-1}=\frac{y-2}{1}=\frac{5+z}{-1}

C

x+3−1=y−21=z+51\frac{x+3}{-1}=\frac{y-2}{1}=\frac{z+5}{1}

D

x+3−1=2−y1=z+5−1\frac{x+3}{-1}=\frac{2-y}{1}=\frac{z+5}{-1}

Answer

Option (c) x+3−1=y−21=z+51\frac{x+3}{-1}=\frac{y-2}{1}=\frac{z+5}{1}

Explanation

Solution

For a line equally inclined to the coordinate axes, its direction cosines (l, m, n) must satisfy

∣l∣=∣m∣=∣n∣|l|=|m|=|n|.

This means the direction ratios are proportional to (±1,±1,±1)(\pm1, \pm1, \pm1). The line must pass through (−3,2,−5)(-3,2,-5), so its symmetric equation will have the form

x+3l=y−2m=z+5n\frac{x+3}{l}=\frac{y-2}{m}=\frac{z+5}{n}

with ∣l∣=∣m∣=∣n∣|l|=|m|=|n|.

Among the given options:

  • Option (a) has direction ratios (2,1,1)(2,1,1) which are not equal in magnitude.
  • Option (b) gives (−1,1,−1)(-1,1,-1), option (c) gives (−1,1,1)(-1,1,1), and option (d) (after rewriting 2−y1=−y−21\frac{2-y}{1}=-\frac{y-2}{1}) gives (−1,−1,−1)(-1,-1,-1). In each of these cases the absolute values are equal.

Typically the desired standard form is one where the denominators are written as they appear in the point form. Option (c) is the most straightforward representation:

x+3−1=y−21=z+51\frac{x+3}{-1}=\frac{y-2}{1}=\frac{z+5}{1}.