Question

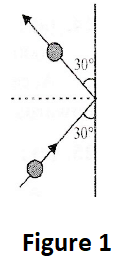
A $0.5kg$ ball moving with a speed of $12m/s\;$ strikes a hard wall at an angle of ${30^o}$ with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for $0.25s\;$ the average force acting on the wall is:

(A) $48N$
(B) $24N$
(C) $12N$
(D) $96N$

Answer 1

The average speed can be defined as the force that is applied to a body that’s travelling at a definite velocity over a definite period of time. We need to write this mathematically and we need to substitute the known values. We are using the term average to specify that this velocity is not accurately measured or instantaneous velocity.
$F{\text{ }} = {\text{ }}\dfrac{{m{\text{ }}({v_{f{\text{ }}-\;}}{v_i})}}{{\Delta \;t}}$
Here, m is said to be the mass of the body
${v_f}$ is the final velocity
${v_i}$ is the initial velocity
$\Delta \;t$ is the change in time.

Complete Step By Step Answer:
Given that the ball moves with an initial velocity of $12m/s\;$ . This hits a wall at an angle ${30^o}$ . The ball’s mass is given as $0.5kg$ .
Here the components of momentums that are parallel to the wall will add each other and the components of momentum that are perpendicular to the wall will be of equal magnitude and opposite in direction.
We know from the above-given formula, change in momentum $=$ $F \times \Delta \;t$
Resolving the momentum along the perpendicular direction we get,
$mv\sin \theta - ( - mv\sin \theta ) = F \times \Delta \;t$
$\Rightarrow F = \dfrac{{2mv\sin \theta }}{{\Delta \;t}}$
Now substituting all the known values in the above equation we get,
$F = \dfrac{{2 \times 0.5 \times 12 \times \sin {{30}^o}}}{{0.25}}$
$\Rightarrow 48 \times \dfrac{1}{2} = 24N$
Therefore the average force is found to be $24N$ .
Correct Answer: Therefore the correct option is B.

Note:
We know that the force is said to be a vector quantity and it has both magnitude and direction. In order to explain a force acting on a body, we need to explain both the magnitude and the direction in which the force acts. For a particular time interval t, the average force can be described as the frequency of the change of momentum. It is seen that it is difficult to determine the rate of change if the time interval is very small.