Question
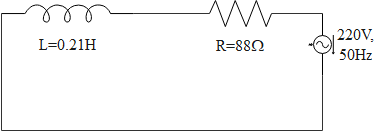
Question: A \(0.21H\) inductor and a \(88\Omega \) resistor are connected in series to a \(220V\) , \(50Hz\) A...
A 0.21H inductor and a 88Ω resistor are connected in series to a 220V , 50Hz AC source. Find out the current in the circuit and the phase angle between the current and the source voltage respectively.
It is recommended to use π=722
A.2A,tan−143B.14.4A,tan−187C.14.4A,tan−178D.3.28A,tan−1112
Solution
The impedance of a circuit can be found by taking the square root of the sum of the squares of resistance and inductive reactance. Using this, find the impedance of the circuit. Then find the current through the circuit. The tangent of the phase angle is given as the inductive reactance divided by the resistance. These may help you to solve this question.
Complete step by step answer:
The impedance of a circuit can be found using the equation,
Z=R2+XL2
Where R be the resistance and XL be the inductive reactance.
It is already mentioned in the question that,
R=88ΩL=0.21H
Where Lbe the inductance of the inductor.
The inductive reactance can be found using the formula,2A
XL=2πfL
f=50Hz
Where fbe the frequency of the circuit
Let us substitute the parameters in the equation,
XL=2π×50×0.21=65.973Ω
So let us use this in the equation of impedance,
Z=882+65.9732=110Ω
Now let us calculate the current flowing through the circuit, which is given as,
I=ZV
Where the voltage is given as,
V=220V
Using this value in the equation of current will give,
I=110220=2A
Now the phase angle is given by the equation,
θ=tan−1(RXL)
Substituting the values of the terms in the equation will give,
θ=tan−1(8865.973)
Simplifying will give,
θ=tan−1(43)
Therefore the current in the circuit is obtained as 2A and the phase angle is obtained asθ=tan−1(43).
Hence the correct answer is option A.
Note:
Inductive reactance is given as the prevention of the variation in current through an element. In an AC circuit, in the case of an ideal inductor, the preventive or the opposition effect on change in current flow will cause a delay or a phase shift. This is happening in the alternating current with respect to their alternating voltage.
