Question
Question: Through the vertex O of the parabola $y^2=4ax$, a perpendicular is drawn to any tangent meeting it a...
Through the vertex O of the parabola y2=4ax, a perpendicular is drawn to any tangent meeting it at P & the parabola at Q. Show that OP⋅OQ = constant.
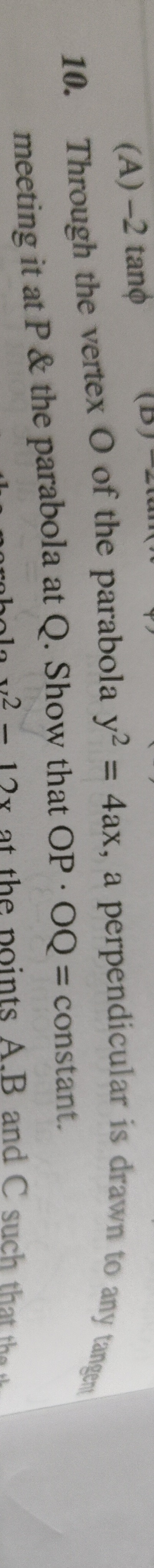
OP⋅OQ=4a2
Solution
The parametric coordinates of a point T on the parabola y2=4ax are (at2,2at). The equation of the tangent at T is yt=a(x+at2), which can be rewritten as x−yt+at2=0.
The line OP is perpendicular to the tangent and passes through the vertex O(0,0). The slope of the tangent is mt=1/t. The slope of OP is mOP=−t. The equation of the line OP is y=−tx.
P is the foot of the perpendicular from O(0,0) to the tangent line x−yt+at2=0. The distance OP is: OP=12+(−t)2∣at2∣=1+t2∣a∣t2
Q is the point where the line OP (y=−tx) intersects the parabola y2=4ax. Substituting y=−tx into the parabola equation: (−tx)2=4ax⟹t2x2=4ax x(t2x−4a)=0 The non-vertex solution is xQ=t24a. The corresponding y-coordinate is yQ=−txQ=−t(t24a)=−t4a. So, the coordinates of Q are (t24a,−t4a).
The distance OQ from the origin O(0,0) to Q is: OQ=(t24a)2+(−t4a)2=t416a2+t216a2=t416a2(1+t2)=t24∣a∣1+t2
Now, we compute the product of OP and OQ: OP⋅OQ=(1+t2∣a∣t2)⋅(t24∣a∣1+t2)=4∣a∣2=4a2 This product is independent of the parameter t, hence it is a constant.
