Solveeit Logo
Login

Question

Question: If $V_1, V_2$ are two orthogonal unit vectors and $V_3 = V_1 \times V_2$ then...

If V1,V2V_1, V_2 are two orthogonal unit vectors and V3=V1×V2V_3 = V_1 \times V_2 then

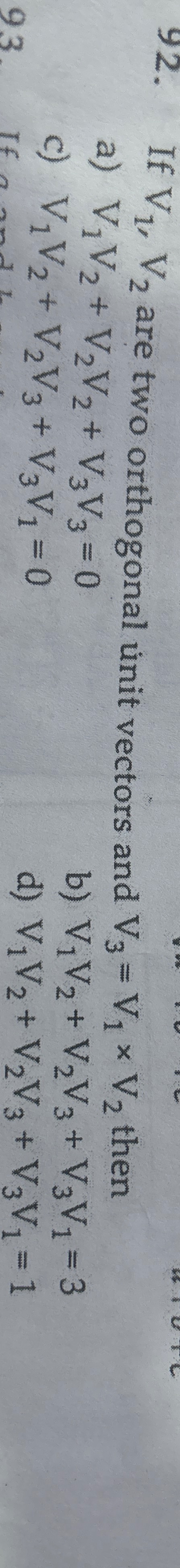
A

V1V2+V2V2+V3V3=0V_1V_2 + V_2V_2 + V_3V_3 = 0

B

V1V2+V2V3+V3V1=3V_1V_2 + V_2V_3 + V_3V_1 = 3

C

V1V2+V2V3+V3V1=0V_1V_2 + V_2V_3 + V_3V_1 = 0

D

V1V2+V2V3+V3V1=1V_1V_2 + V_2V_3 + V_3V_1 = 1

Answer

Option c) is correct.

Explanation

Solution

Given:

  • V1\mathbf{V}_1 and V2\mathbf{V}_2 are orthogonal unit vectors so that V1⋅V1=1,V2⋅V2=1,V1⋅V2=0.\mathbf{V}_1 \cdot \mathbf{V}_1 = 1,\quad \mathbf{V}_2 \cdot \mathbf{V}_2 = 1,\quad \mathbf{V}_1 \cdot \mathbf{V}_2 = 0.
  • Let V3=V1×V2\mathbf{V}_3 = \mathbf{V}_1 \times \mathbf{V}_2. Then, V3\mathbf{V}_3 is a unit vector orthogonal to both, so V1⋅V3=0,V2⋅V3=0.\mathbf{V}_1 \cdot \mathbf{V}_3 = 0,\quad \mathbf{V}_2 \cdot \mathbf{V}_3 = 0.

Checking each option:

  • Option a): V1V2+V2V2+V3V3\mathbf{V}_1\mathbf{V}_2 + \mathbf{V}_2\mathbf{V}_2 + \mathbf{V}_3\mathbf{V}_3

    Interpreting juxtaposed vectors as dot products:

    V1⋅V2+V2⋅V2+V3⋅V3=0+1+1=2≠0.\mathbf{V}_1 \cdot \mathbf{V}_2 + \mathbf{V}_2 \cdot \mathbf{V}_2 + \mathbf{V}_3 \cdot \mathbf{V}_3 = 0 + 1 + 1 = 2 \neq 0.

    So, option a) is false.

  • Option c): V1V2+V2V3+V3V1\mathbf{V}_1\mathbf{V}_2 + \mathbf{V}_2\mathbf{V}_3 + \mathbf{V}_3\mathbf{V}_1

    Evaluating:

    V1⋅V2+V2⋅V3+V3⋅V1=0+0+0=0.\mathbf{V}_1 \cdot \mathbf{V}_2 + \mathbf{V}_2 \cdot \mathbf{V}_3 + \mathbf{V}_3 \cdot \mathbf{V}_1 = 0 + 0 + 0 = 0.

    So, option c) is true.

  • Options b) and d) provide sums 3 and 1 respectively for the same expression as in option c), hence they are false.