Question
Question: Let $a = \sum_{r=1}^{\infty} \frac{1}{r^2}$ and $b = \sum_{r=1}^{\infty} \frac{1}{(2r-1)^2}$. Then t...
Let a=∑r=1∞r21 and b=∑r=1∞(2r−1)21. Then the value of b3a is equal to:
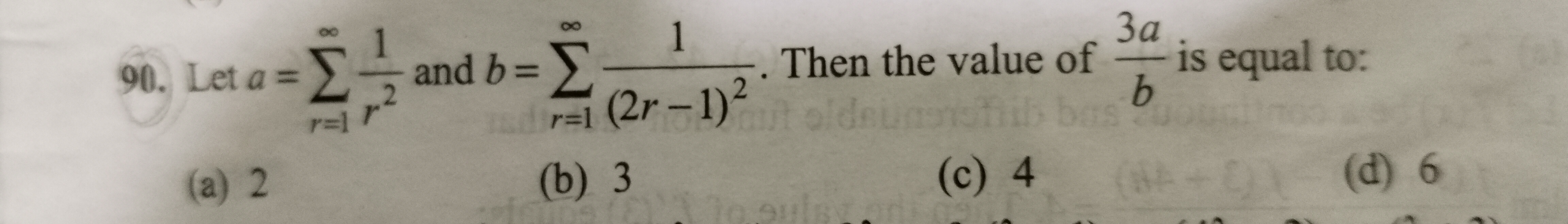
2
3
4
6
4
Solution
The given series are: a=∑r=1∞r21=121+221+321+421+… b=∑r=1∞(2r−1)21=121+321+521+…
We can express the series a by separating terms with odd and even denominators: a=(121+321+521+…)+(221+421+621+…)
The first parenthesis is the series b. The second parenthesis is the sum of reciprocals of squares of even numbers. This can be written as: ∑r=1∞(2r)21=∑r=1∞4r21=41∑r=1∞r21=41a Substituting these back into the expression for a: a=b+41a Rearranging the equation to solve for b: b=a−41a=43a We are asked to find the value of b3a. Substitute the expression for b: b3a=43a3a Since a is a convergent series (a=6π2=0), we can cancel a from the numerator and denominator: b3a=433=3×34=4
