Question

Which of the following option(s) is/are correct

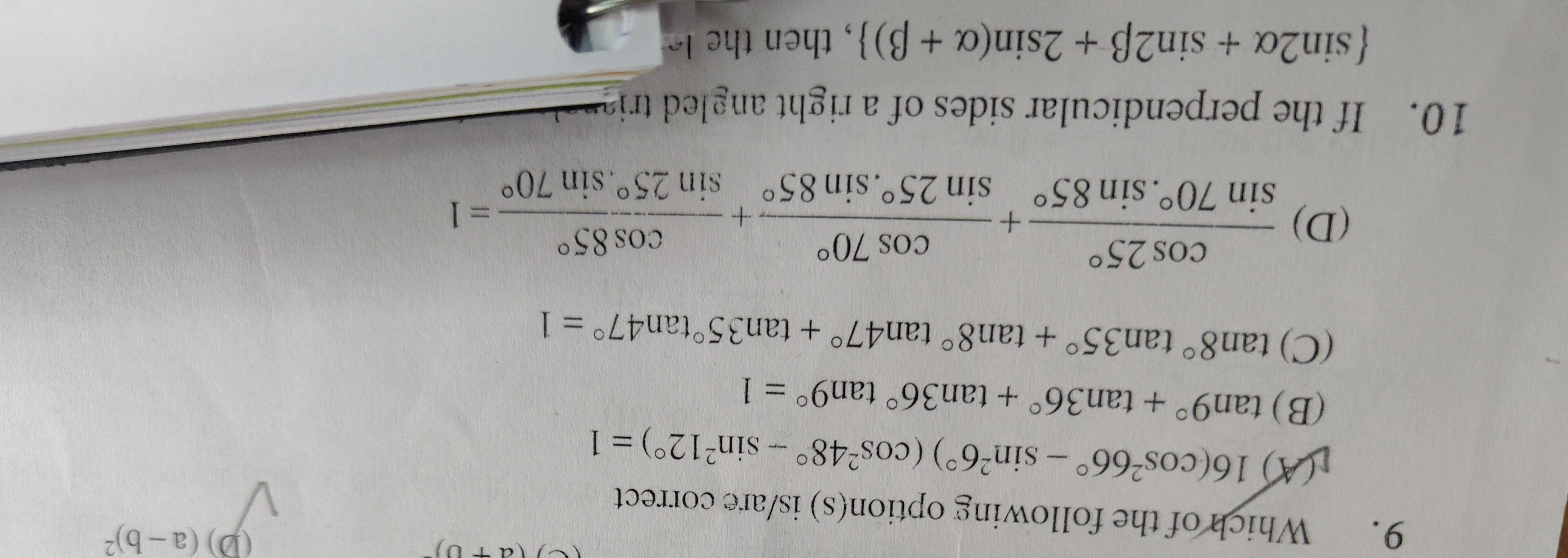
• A. 16(cos²66° - sin²6°) (cos²48° - sin²12°) = 1
• B. tan9° + tan36° + tan36° tan9° = 1
• C. tan8° tan35° + tan8° tan47° + tan35°tan47° = 1
• D. $\frac{sin 70°. sin 85°}{cos 25°} + \frac{sin 25°.sin 85°}{cos 70°} + \frac{sin 25°. sin 70°}{cos 85°}$ = 1

Answer 1

Answer: (A), (B), (C)

A, B, C

Answer 2

The problem asks us to identify the correct option(s) among the given trigonometric expressions. We will evaluate each option individually.

Option (A): The expression is $16(\cos^266^\circ - \sin^26^\circ)(\cos^248^\circ - \sin^212^\circ)$. We use the trigonometric identity: $\cos^2A - \sin^2B = \cos(A+B)\cos(A-B)$.

For the first term: $\cos^266^\circ - \sin^26^\circ$ Here, $A=66^\circ$ and $B=6^\circ$. So, $\cos^266^\circ - \sin^26^\circ = \cos(66^\circ+6^\circ)\cos(66^\circ-6^\circ) = \cos(72^\circ)\cos(60^\circ)$.

For the second term: $\cos^248^\circ - \sin^212^\circ$ Here, $A=48^\circ$ and $B=12^\circ$. So, $\cos^248^\circ - \sin^212^\circ = \cos(48^\circ+12^\circ)\cos(48^\circ-12^\circ) = \cos(60^\circ)\cos(36^\circ)$.

Substitute these back into the expression: $16[\cos(72^\circ)\cos(60^\circ)][\cos(60^\circ)\cos(36^\circ)]$ We know $\cos(60^\circ) = \frac{1}{2}$. $= 16 \cdot \cos(72^\circ) \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \cos(36^\circ)$ $= 16 \cdot \frac{1}{4} \cdot \cos(72^\circ)\cos(36^\circ)$ $= 4 \cos(72^\circ)\cos(36^\circ)$

Now, we use the known values: $\cos(36^\circ) = \frac{\sqrt{5}+1}{4}$ $\cos(72^\circ) = \frac{\sqrt{5}-1}{4}$

Substitute these values: $= 4 \left( \frac{\sqrt{5}-1}{4} \right) \left( \frac{\sqrt{5}+1}{4} \right)$ $= 4 \left( \frac{(\sqrt{5})^2 - 1^2}{16} \right)$ $= 4 \left( \frac{5 - 1}{16} \right)$ $= 4 \left( \frac{4}{16} \right)$ $= 4 \cdot \frac{1}{4} = 1$ So, option (A) is correct.

Option (B): The expression is $\tan9^\circ + \tan36^\circ + \tan36^\circ \tan9^\circ = 1$. Consider the identity for $\tan(A+B)$: $\tan(A+B) = \frac{\tan A + \tan B}{1 - \tan A \tan B}$ Rearranging this, we get: $\tan A + \tan B = \tan(A+B)(1 - \tan A \tan B)$ $\tan A + \tan B = \tan(A+B) - \tan(A+B)\tan A \tan B$ $\tan A + \tan B + \tan(A+B)\tan A \tan B = \tan(A+B)$

If $A+B = 45^\circ$, then $\tan(A+B) = \tan(45^\circ) = 1$. Substituting $\tan(A+B) = 1$ into the rearranged identity: $\tan A + \tan B + 1 \cdot \tan A \tan B = 1$ $\tan A + \tan B + \tan A \tan B = 1$

In the given expression, $A=9^\circ$ and $B=36^\circ$. $A+B = 9^\circ + 36^\circ = 45^\circ$. Since $A+B=45^\circ$, the identity $\tan A + \tan B + \tan A \tan B = 1$ holds true. So, option (B) is correct.

Option (C): The expression is $\tan8^\circ \tan35^\circ + \tan8^\circ \tan47^\circ + \tan35^\circ\tan47^\circ = 1$. Consider the identity for $\tan(A+B+C)$: $\tan(A+B+C) = \frac{\tan A + \tan B + \tan C - \tan A \tan B \tan C}{1 - (\tan A \tan B + \tan B \tan C + \tan C \tan A)}$

If $A+B+C = 90^\circ$, then $\tan(A+B+C)$ is undefined. This implies that the denominator must be zero. $1 - (\tan A \tan B + \tan B \tan C + \tan C \tan A) = 0$ $\tan A \tan B + \tan B \tan C + \tan C \tan A = 1$

In the given expression, $A=8^\circ$, $B=35^\circ$, and $C=47^\circ$. $A+B+C = 8^\circ + 35^\circ + 47^\circ = 90^\circ$. Since $A+B+C=90^\circ$, the identity $\tan A \tan B + \tan B \tan C + \tan C \tan A = 1$ holds true. So, option (C) is correct.

Option (D): The expression is $\frac{\sin 70^\circ \sin 85^\circ}{\cos 25^\circ} + \frac{\sin 25^\circ \sin 85^\circ}{\cos 70^\circ} + \frac{\sin 25^\circ \sin 70^\circ}{\cos 85^\circ} = 1$. Let $A=25^\circ$, $B=70^\circ$, $C=85^\circ$. Note that $A+B+C = 25^\circ+70^\circ+85^\circ = 180^\circ$. This means A, B, C are angles of a triangle. In a triangle, $\cos A = \cos(180^\circ - (B+C)) = -\cos(B+C)$. Similarly, $\cos B = -\cos(A+C)$ and $\cos C = -\cos(A+B)$.

The expression can be written as: $\frac{\sin B \sin C}{\cos A} + \frac{\sin A \sin C}{\cos B} + \frac{\sin A \sin B}{\cos C}$ $= \frac{\sin B \sin C}{-\cos(B+C)} + \frac{\sin A \sin C}{-\cos(A+C)} + \frac{\sin A \sin B}{-\cos(A+B)}$

Let's test with a simpler case, e.g., an equilateral triangle where $A=B=C=60^\circ$. $\cos 60^\circ = 1/2$, $\sin 60^\circ = \sqrt{3}/2$. The expression becomes: $3 \times \frac{\sin 60^\circ \sin 60^\circ}{\cos 60^\circ} = 3 \times \frac{(\sqrt{3}/2)(\sqrt{3}/2)}{1/2}$ $= 3 \times \frac{3/4}{1/2} = 3 \times \frac{3}{4} \times 2 = 3 \times \frac{3}{2} = \frac{9}{2}$. Since $9/2 \neq 1$, the identity does not hold true in general for a triangle, and therefore not for the given angles. So, option (D) is incorrect.

Based on the analysis, options (A), (B), and (C) are correct.