Question

Two tangents to the parabola $y^2 = 8x$ meet the tangent at its vertex in the points P and Q. If PQ = 4, then find the locus of the point of the intersection of these two tangents.

Answer 1

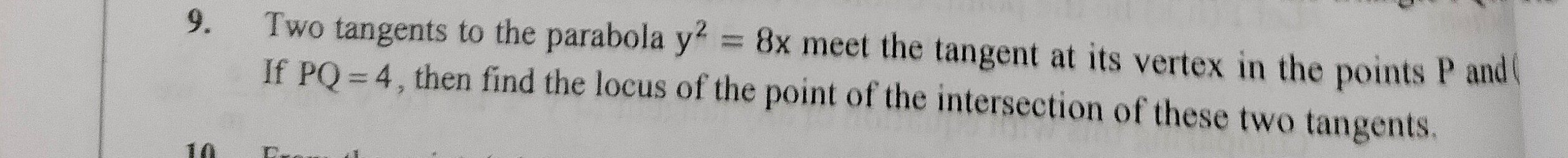
y^2 = 8(x+2)

Answer 2

The given parabola is $y^2 = 8x$. Comparing this with the standard form $y^2 = 4ax$, we have $4a = 8$, which gives $a = 2$. The vertex of the parabola is at $(0, 0)$. The tangent at the vertex is the y-axis, which has the equation $x = 0$.

Let the two tangents to the parabola intersect at point $T(h, k)$. Let these tangents touch the parabola at points with parameters $t_1$ and $t_2$. The coordinates of a point on the parabola $y^2 = 4ax$ can be represented as $(at^2, 2at)$. For $y^2 = 8x$ (where $a=2$), the points are $(2t^2, 4t)$.

The equation of the tangent to the parabola $y^2 = 4ax$ at the point $(at^2, 2at)$ is given by $yt = x/a + at$. For $y^2 = 8x$ ($a=2$), the tangent equation is $yt = x/2 + 2t$, which can be rewritten as $yt = x + 2t^2$.

Let the two tangents be $T_1$ and $T_2$, touching the parabola at points with parameters $t_1$ and $t_2$ respectively. The equation of $T_1$ is $yt_1 = x + 2t_1^2$. The equation of $T_2$ is $yt_2 = x + 2t_2^2$.

The point P is the intersection of tangent $T_1$ with the tangent at the vertex ($x=0$). Substituting $x=0$ into the equation for $T_1$: $yt_1 = 0 + 2t_1^2$. If $t_1 \neq 0$, then $y = 2t_1$. So, point P has coordinates $(0, 2t_1)$.

The point Q is the intersection of tangent $T_2$ with the tangent at the vertex ($x=0$). Substituting $x=0$ into the equation for $T_2$: $yt_2 = 0 + 2t_2^2$. If $t_2 \neq 0$, then $y = 2t_2$. So, point Q has coordinates $(0, 2t_2)$.

The points P and Q lie on the y-axis. The distance between P and Q is given as 4. $PQ = |y_P - y_Q| = |2t_1 - 2t_2| = 2|t_1 - t_2|$. We are given $PQ = 4$, so $2|t_1 - t_2| = 4$, which implies $|t_1 - t_2| = 2$. Squaring both sides, we get $(t_1 - t_2)^2 = 4$.

Now, let's find the coordinates of the point of intersection $T(h, k)$ of the tangents $T_1$ and $T_2$. $yt_1 = x + 2t_1^2 \quad (1)$ $yt_2 = x + 2t_2^2 \quad (2)$ Subtracting (2) from (1): $y(t_1 - t_2) = 2(t_1^2 - t_2^2) = 2(t_1 - t_2)(t_1 + t_2)$. Assuming $t_1 \neq t_2$ (which is necessary for distinct tangents), we can divide by $(t_1 - t_2)$: $y = 2(t_1 + t_2)$. So, the y-coordinate of the intersection point is $k = 2(t_1 + t_2)$.

Substitute $y=k$ into equation (1): $kt_1 = x + 2t_1^2$. $x = kt_1 - 2t_1^2$. Substitute $k = 2(t_1 + t_2)$: $x = 2(t_1 + t_2)t_1 - 2t_1^2 = 2t_1^2 + 2t_1t_2 - 2t_1^2 = 2t_1t_2$. So, the x-coordinate of the intersection point is $h = 2t_1t_2$.

The point of intersection is $T(h, k) = (2t_1t_2, 2(t_1 + t_2))$. We have the relations: $h = 2t_1t_2 \implies t_1t_2 = h/2$. $k = 2(t_1 + t_2) \implies t_1 + t_2 = k/2$.

We use the identity $(t_1 + t_2)^2 - (t_1 - t_2)^2 = 4t_1t_2$. Substitute the expressions in terms of $h$ and $k$, and the given condition $(t_1 - t_2)^2 = 4$: $(\frac{k}{2})^2 - 4 = 4(\frac{h}{2})$. $\frac{k^2}{4} - 4 = 2h$.

To find the locus, we rearrange this equation: Multiply the entire equation by 4: $k^2 - 16 = 8h$. $k^2 = 8h + 16$. $k^2 = 8(h + 2)$.

Replacing $(h, k)$ with $(x, y)$ to represent the locus: $y^2 = 8(x + 2)$.