Question
Question: Two mutually perpendicular tangents of the parabola $y^2=4ax$ meet its axis in $P_1$ and $P_2$. If S...
Two mutually perpendicular tangents of the parabola y2=4ax meet its axis in P1 and P2. If S is the focus of the parabola then SP11+SP21 is equal to :
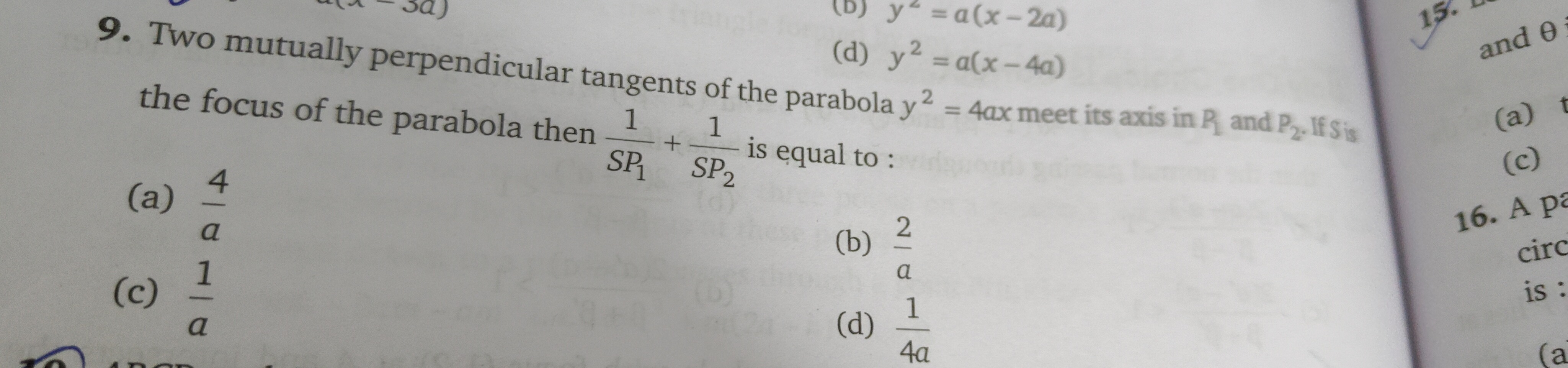
a4
a2
a1
4a1
a1
Solution
The focus of the parabola y2=4ax is S=(a,0). The axis is the x-axis. The equation of a tangent to the parabola in parametric form is yt=x+at2. When this tangent meets the axis (y=0), we have 0=x+at2, so x=−at2. Let the points where the two perpendicular tangents meet the axis be P1=(−at12,0) and P2=(−at22,0). The slope of the tangent x−yt+at2=0 is m=t1. For perpendicular tangents, m1m2=−1, which means t11⋅t21=−1, so t1t2=−1. This implies t2=−t11, and thus t22=t121. The distances from the focus S(a,0) to P1 and P2 are: SP1=∣a−(−at12)∣=∣a(1+t12)∣ SP2=∣a−(−at22)∣=∣a(1+t22)∣=∣a(1+t121)∣=∣at12t12+1∣ We need to find SP11+SP21: SP11=∣a(1+t12)∣1 SP21=∣at12t12+1∣1=∣a(t12+1)∣t12 SP11+SP21=∣a(1+t12)∣1+∣a(t12+1)∣t12=∣a(1+t12)∣1+t12 Since 1+t12>0, this simplifies to ∣a∣(1+t12)1+t12=∣a∣1. Assuming a>0 (as is standard and implied by the options), the result is a1.
