Question

Two identical positive point charges 'q' are placed on the x-axis at x = -a and x = +a respectively as shown. A point 'p' on the y-axis is chosen where the electric field has maximum strength $E_0$. Value of $E_0$ is

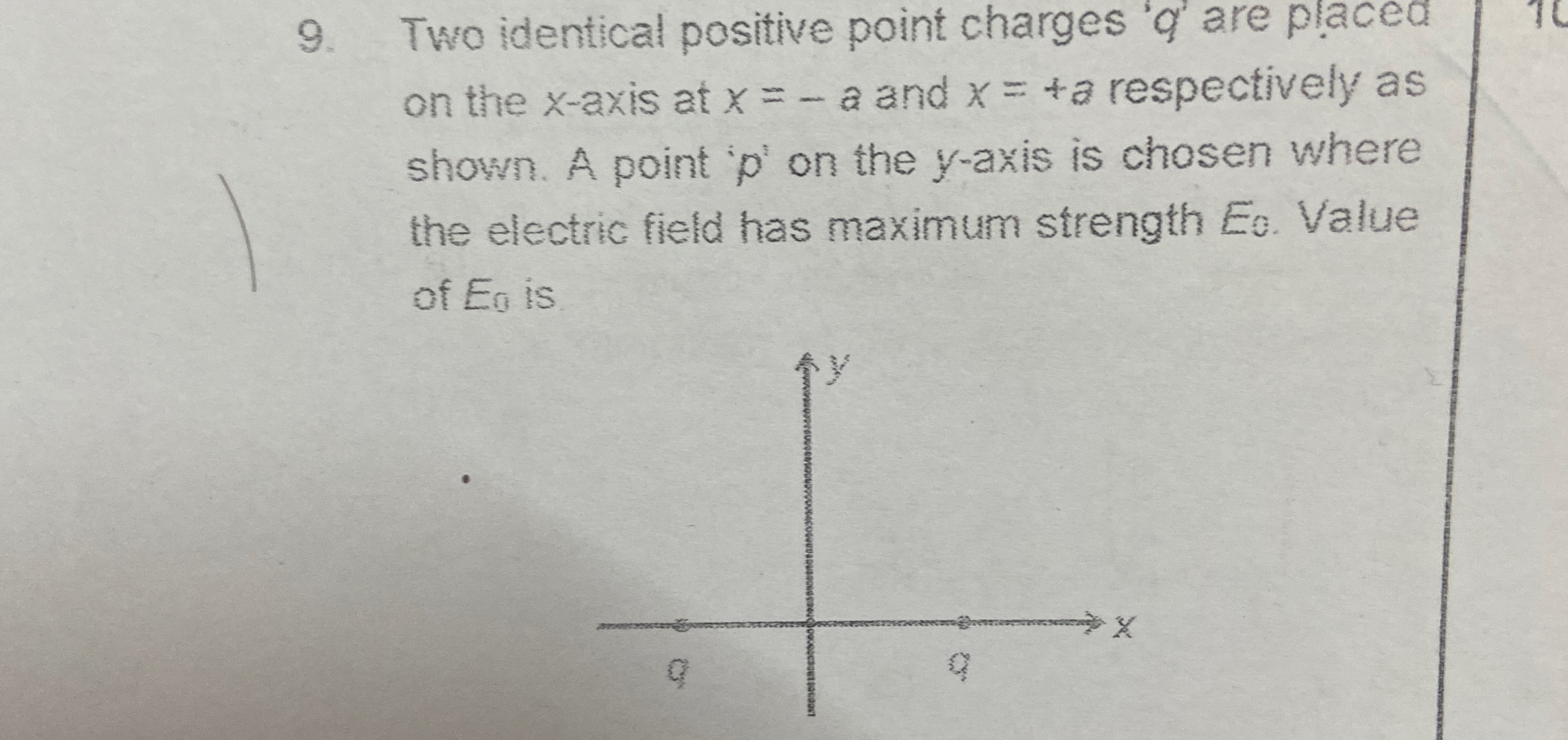
Answer 1

E_0 = \frac{4kq}{3\sqrt{3},a^2}.

Answer 2

The net electric field at point $P(0,y)$ due to two charges at $(a,0)$ and $(-a,0)$ is obtained by adding the vertical components because the horizontal components cancel. The field from one charge is

$$E = \frac{kq}{r^2},\quad \text{with } r = \sqrt{a^2+y^2},$$

and its vertical component is

$$E_y = \frac{kq\,y}{(a^2+y^2)^{3/2}}.$$

Thus, the total field is

$$E_{\text{net}} = 2\,\frac{kq\,y}{(a^2+y^2)^{3/2}}.$$

To maximize $E_{\text{net}}$ with respect to $y$, differentiate

$$f(y)=\frac{y}{(a^2+y^2)^{3/2}}$$

and set the derivative equal to zero:

$$\frac{d}{dy}\left(\frac{y}{(a^2+y^2)^{3/2}}\right)=\frac{(a^2+y^2)-3y^2}{(a^2+y^2)^{5/2}}=0.$$

This gives

$$a^2 - 2y^2 = 0 \quad \Rightarrow \quad y = \frac{a}{\sqrt{2}}.$$

Substitute $y = \frac{a}{\sqrt{2}}$ into the expression for $E_{\text{net}}$:

$$E_0 = 2\,\frac{kq\,\frac{a}{\sqrt{2}}}{\left(a^2+\frac{a^2}{2}\right)^{3/2}} = \frac{2kq\,a/\sqrt{2}}{\left(\frac{3a^2}{2}\right)^{3/2}} = \frac{2kq\,a/\sqrt{2}}{\frac{3^{3/2}a^3}{2^{3/2}}}.$$

Simplify:

$$E_0 = \frac{2kq\,a}{\sqrt{2}} \cdot \frac{2^{3/2}}{3^{3/2}a^3} = \frac{2kq\,a\cdot 2\sqrt{2}}{\sqrt{2}\,3^{3/2}a^3} = \frac{4kq}{3^{3/2}a^2} = \frac{4kq}{3\sqrt{3}\,a^2}.$$