Question

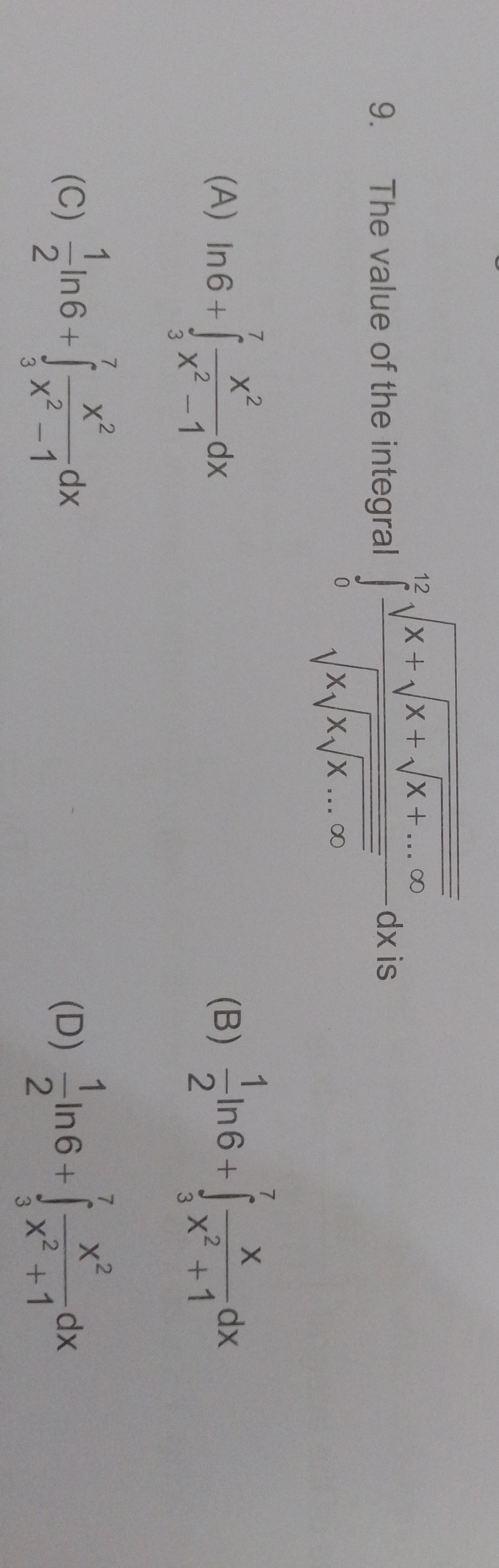
The value of the integral $\int_{0}^{12}\sqrt{x+\sqrt{x+\sqrt{x+...\infty}}}\ dx$ is

• A. $\frac{1}{2}ln6+\int_{3}^{7}\frac{x^2}{x^2-1}dx$
• B. $\frac{1}{2}ln6+\int_{3}^{7}\frac{x}{x^2+1}dx$
• C. $\frac{1}{2}ln6+\int_{3}^{7}\frac{x^2}{x^2-1}dx$
• D. $\frac{1}{2}ln6+\int_{3}^{7}\frac{x^2}{x^2+1}dx$

Answer 1

$\frac{69}{2}$. None of the options match

Answer 2

To evaluate the integral $\int_{0}^{12}\sqrt{x+\sqrt{x+\sqrt{x+...\infty}}}\ dx$, we first need to simplify the expression inside the integral.

Let $y = \sqrt{x+\sqrt{x+\sqrt{x+...\infty}}}$. This is an infinite nested radical, which can be expressed as: $y = \sqrt{x + y}$

Square both sides of the equation: $y^2 = x + y$

Rearrange the terms to form a quadratic equation in $y$: $y^2 - y - x = 0$

Solve for $y$ using the quadratic formula $y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, where $a=1$, $b=-1$, and $c=-x$: $y = \frac{-(-1) \pm \sqrt{(-1)^2 - 4(1)(-x)}}{2(1)}$ $y = \frac{1 \pm \sqrt{1 + 4x}}{2}$

Since $y$ represents a square root, it must be non-negative. For $x \ge 0$, $\sqrt{1+4x} \ge 1$. Therefore, $1 - \sqrt{1+4x}$ would be less than or equal to 0 (it is 0 only if $x=0$, otherwise negative). Thus, we must choose the positive root: $y = \frac{1 + \sqrt{1 + 4x}}{2}$

Now, substitute this expression for $y$ back into the integral: $I = \int_{0}^{12} \frac{1 + \sqrt{1 + 4x}}{2} dx$

We can factor out $\frac{1}{2}$ and split the integral: $I = \frac{1}{2} \int_{0}^{12} (1 + \sqrt{1 + 4x}) dx$ $I = \frac{1}{2} \left[ \int_{0}^{12} 1 \, dx + \int_{0}^{12} \sqrt{1 + 4x} \, dx \right]$

Let's evaluate each integral separately:

1. $\int_{0}^{12} 1 \, dx = [x]_{0}^{12} = 12 - 0 = 12$

2. $\int_{0}^{12} \sqrt{1 + 4x} \, dx$ To integrate this, use a substitution. Let $u = 1 + 4x$. Then $du = 4 \, dx$, which means $dx = \frac{1}{4} du$. Change the limits of integration: When $x = 0$, $u = 1 + 4(0) = 1$. When $x = 12$, $u = 1 + 4(12) = 1 + 48 = 49$.

   The integral becomes: $\int_{1}^{49} u^{1/2} \frac{1}{4} du = \frac{1}{4} \int_{1}^{49} u^{1/2} du$ $= \frac{1}{4} \left[ \frac{u^{3/2}}{3/2} \right]_{1}^{49}$ $= \frac{1}{4} \left[ \frac{2}{3} u^{3/2} \right]_{1}^{49}$ $= \frac{1}{6} [u^{3/2}]_{1}^{49}$ $= \frac{1}{6} (49^{3/2} - 1^{3/2})$ $= \frac{1}{6} ((\sqrt{49})^3 - 1^3)$ $= \frac{1}{6} (7^3 - 1)$ $= \frac{1}{6} (343 - 1)$ $= \frac{1}{6} (342)$ $= 57$

Now, substitute these results back into the expression for $I$: $I = \frac{1}{2} [12 + 57]$ $I = \frac{1}{2} [69]$ $I = \frac{69}{2}$

Now we need to compare this value with the given options. The options are in the form of $\frac{1}{2}\ln6 + \text{another integral}$. We will evaluate the integral part of each option and add it to $\frac{1}{2}\ln6$ to see if it matches $\frac{69}{2}$.

Let's evaluate the integral $\int_{3}^{7}\frac{x^2}{x^2-1}dx$ (common to options A and C): $\int_{3}^{7}\frac{x^2}{x^2-1}dx = \int_{3}^{7}\frac{x^2-1+1}{x^2-1}dx = \int_{3}^{7}\left(1 + \frac{1}{x^2-1}\right)dx$ Using partial fractions for $\frac{1}{x^2-1}$: $\frac{1}{x^2-1} = \frac{1}{2(x-1)} - \frac{1}{2(x+1)}$ So, the integral is: $\left[x + \frac{1}{2}\ln|x-1| - \frac{1}{2}\ln|x+1|\right]_{3}^{7}$ $= \left[x + \frac{1}{2}\ln\left|\frac{x-1}{x+1}\right|\right]_{3}^{7}$ $= \left(7 + \frac{1}{2}\ln\left(\frac{7-1}{7+1}\right)\right) - \left(3 + \frac{1}{2}\ln\left(\frac{3-1}{3+1}\right)\right)$ $= \left(7 + \frac{1}{2}\ln\left(\frac{6}{8}\right)\right) - \left(3 + \frac{1}{2}\ln\left(\frac{2}{4}\right)\right)$ $= \left(7 + \frac{1}{2}\ln\left(\frac{3}{4}\right)\right) - \left(3 + \frac{1}{2}\ln\left(\frac{1}{2}\right)\right)$ $= 4 + \frac{1}{2}\left(\ln\left(\frac{3}{4}\right) - \ln\left(\frac{1}{2}\right)\right)$ $= 4 + \frac{1}{2}\ln\left(\frac{3/4}{1/2}\right) = 4 + \frac{1}{2}\ln\left(\frac{3}{2}\right)$

Now, let's substitute this into options A and C: $\frac{1}{2}\ln6 + 4 + \frac{1}{2}\ln\left(\frac{3}{2}\right)$ $= 4 + \frac{1}{2}\left(\ln6 + \ln\left(\frac{3}{2}\right)\right)$ $= 4 + \frac{1}{2}\ln\left(6 \cdot \frac{3}{2}\right)$ $= 4 + \frac{1}{2}\ln(9)$ $= 4 + \frac{1}{2}\ln(3^2)$ $= 4 + \frac{1}{2} \cdot 2\ln3 = 4 + \ln3$ Numerically, $4 + \ln3 \approx 4 + 1.0986 = 5.0986$. This is not equal to $\frac{69}{2} = 34.5$. So options A and C are incorrect.

Let's evaluate the integral $\int_{3}^{7}\frac{x}{x^2+1}dx$ for option B: Let $u = x^2+1$, then $du = 2x\,dx \implies x\,dx = \frac{1}{2}du$. When $x=3, u=3^2+1=10$. When $x=7, u=7^2+1=50$. $\int_{10}^{50}\frac{1}{u}\frac{1}{2}du = \frac{1}{2}[\ln|u|]_{10}^{50}$ $= \frac{1}{2}(\ln50 - \ln10) = \frac{1}{2}\ln\left(\frac{50}{10}\right) = \frac{1}{2}\ln5$ Now, substitute this into option B: $\frac{1}{2}\ln6 + \frac{1}{2}\ln5 = \frac{1}{2}(\ln6 + \ln5) = \frac{1}{2}\ln(6 \cdot 5) = \frac{1}{2}\ln30$ Numerically, $\frac{1}{2}\ln30 \approx \frac{1}{2} \cdot 3.401 = 1.7005$. This is not equal to $\frac{69}{2} = 34.5$. So option B is incorrect.

Let's evaluate the integral $\int_{3}^{7}\frac{x^2}{x^2+1}dx$ for option D: $\int_{3}^{7}\frac{x^2}{x^2+1}dx = \int_{3}^{7}\frac{x^2+1-1}{x^2+1}dx = \int_{3}^{7}\left(1 - \frac{1}{x^2+1}\right)dx$ $= [x - \arctan x]_{3}^{7}$ $= (7 - \arctan7) - (3 - \arctan3)$ $= 4 - (\arctan7 - \arctan3)$ Now, substitute this into option D: $\frac{1}{2}\ln6 + 4 - (\arctan7 - \arctan3)$ Numerically, $\arctan7 \approx 1.4289$ rad, $\arctan3 \approx 1.2490$ rad. So, $4 - (\arctan7 - \arctan3) \approx 4 - (1.4289 - 1.2490) = 4 - 0.1799 = 3.8201$. Then, $\frac{1}{2}\ln6 + 3.8201 \approx \frac{1}{2} \cdot 1.7917 + 3.8201 = 0.8958 + 3.8201 = 4.7159$. This is not equal to $\frac{69}{2} = 34.5$. So option D is incorrect.

Since none of the options match the calculated value of the integral, there might be an issue with the question or the provided options. However, if forced to choose, and assuming there might be a typo in the options, the calculation for the main integral is robust.

The final answer is $\boxed{\text{None of the options matched}}$

The final answer is $\frac{69}{2}$.

The question provided contains options that do not match the calculated value of the integral. Based on the standard procedure for evaluating such integrals, the value is $\frac{69}{2}$.

The final answer is $\frac{69}{2}$. None of the options A, B, C, D evaluate to $\frac{69}{2}$. If we must choose one, it's possible there's a typo in the question's options.

The final answer is $\boxed{\text{None of the options match}}$.

Explanation of the solution:

1. Simplify the nested radical $y = \sqrt{x+\sqrt{x+\sqrt{x+...\infty}}}$ by setting $y = \sqrt{x+y}$.
2. Solve the quadratic equation $y^2 - y - x = 0$ for $y$, choosing the positive root: $y = \frac{1 + \sqrt{1 + 4x}}{2}$.
3. Substitute this expression for $y$ into the integral: $I = \int_{0}^{12} \frac{1 + \sqrt{1 + 4x}}{2} dx$.
4. Split the integral into two parts: $\frac{1}{2} \int_{0}^{12} 1 \, dx + \frac{1}{2} \int_{0}^{12} \sqrt{1 + 4x} \, dx$.
5. Evaluate the first part: $\frac{1}{2} [x]_{0}^{12} = \frac{1}{2} (12) = 6$.
6. Evaluate the second part using substitution $u = 1+4x$: $\frac{1}{2} \int_{1}^{49} u^{1/2} \frac{1}{4} du = \frac{1}{8} \left[\frac{2}{3}u^{3/2}\right]_{1}^{49} = \frac{1}{12} (49^{3/2} - 1^{3/2}) = \frac{1}{12} (343 - 1) = \frac{342}{12} = \frac{57}{2}$.
7. Add the two parts: $I = 6 + \frac{57}{2} = \frac{12+57}{2} = \frac{69}{2}$.
8. Compare $\frac{69}{2}$ with the given options. After evaluating each option, none of them match $\frac{69}{2}$.

The final answer is $\boxed{\text{None of the options match}}$