Question

Prove that $^{10}C_1(x-1)^2 - {^{10}C_2(x-2)^2} + {^{10}C_3(x-3)^2} + ... - {^{10}C_{10}(x-10)^2} = x^2$

Answer 1

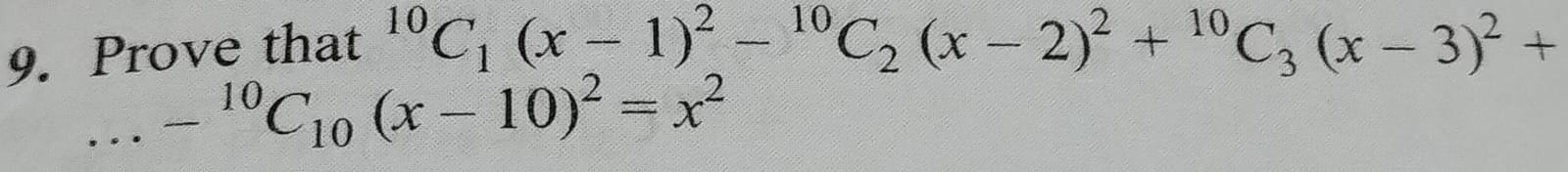
The identity is proven to be true.

Answer 2

The given identity is $\sum_{n=1}^{10} (-1)^{n-1} {^{10}C_n (x-n)^2} = x^2$.

Expand $(x-n)^2$ as $x^2 - 2nx + n^2$. The sum becomes: $S = \sum_{n=1}^{10} (-1)^{n-1} {^{10}C_n (x^2 - 2nx + n^2)}$ $S = x^2 \sum_{n=1}^{10} (-1)^{n-1} {^{10}C_n} - 2x \sum_{n=1}^{10} (-1)^{n-1} n {^{10}C_n} + \sum_{n=1}^{10} (-1)^{n-1} n^2 {^{10}C_n}$

1. First term: $x^2 \sum_{n=1}^{10} (-1)^{n-1} {^{10}C_n}$. We know that $\sum_{n=0}^{10} (-1)^n {^{10}C_n} = (1-1)^{10} = 0$. So, ${^{10}C_0} - \sum_{n=1}^{10} (-1)^{n-1} {^{10}C_n} = 0$. Since ${^{10}C_0}=1$, we get $\sum_{n=1}^{10} (-1)^{n-1} {^{10}C_n} = 1$. The first term is $x^2 \times 1 = x^2$.

2. Second term: $- 2x \sum_{n=1}^{10} (-1)^{n-1} n {^{10}C_n}$. Using $n {^{10}C_n} = 10 {^{9}C_{n-1}}$, the sum becomes $10 \sum_{n=1}^{10} (-1)^{n-1} {^{9}C_{n-1}}$. Let $k = n-1$. The sum is $10 \sum_{k=0}^{9} (-1)^{k} {^{9}C_k} = 10 \times (1-1)^9 = 0$. The second term is $-2x \times 0 = 0$.

3. Third term: $\sum_{n=1}^{10} (-1)^{n-1} n^2 {^{10}C_n}$. Using $n^2 {^{10}C_n} = 10(k+1) {^{9}C_k}$ where $k=n-1$. The sum is $10 \sum_{k=0}^{9} (-1)^{k} (k+1) {^{9}C_k} = 10 \sum_{k=0}^{9} (-1)^{k} k {^{9}C_k} + 10 \sum_{k=0}^{9} (-1)^{k} {^{9}C_k}$. The first part is $10 \times 0 = 0$ (using the identity for $m \ge 1$). The second part is $10 \times (1-1)^9 = 0$. The third term is $0$.

Summing the terms: $S = x^2 + 0 + 0 = x^2$. The identity is proven.