Question

Plane rectangular loop is placed in a magnetic field. The loop was pulled out of the magnetic field at a velocity which is not constant. Assume the magnetic induction in the region is $\overrightarrow{B}$ and it is uniform and constant. The EMF induced in the loop due to this field is $\varepsilon_i$ whose maximum value is $\varepsilon_m$. Now $\varepsilon_i$ is plotted against time t as shown in the graph. Which of the following are/is correct statement(s):

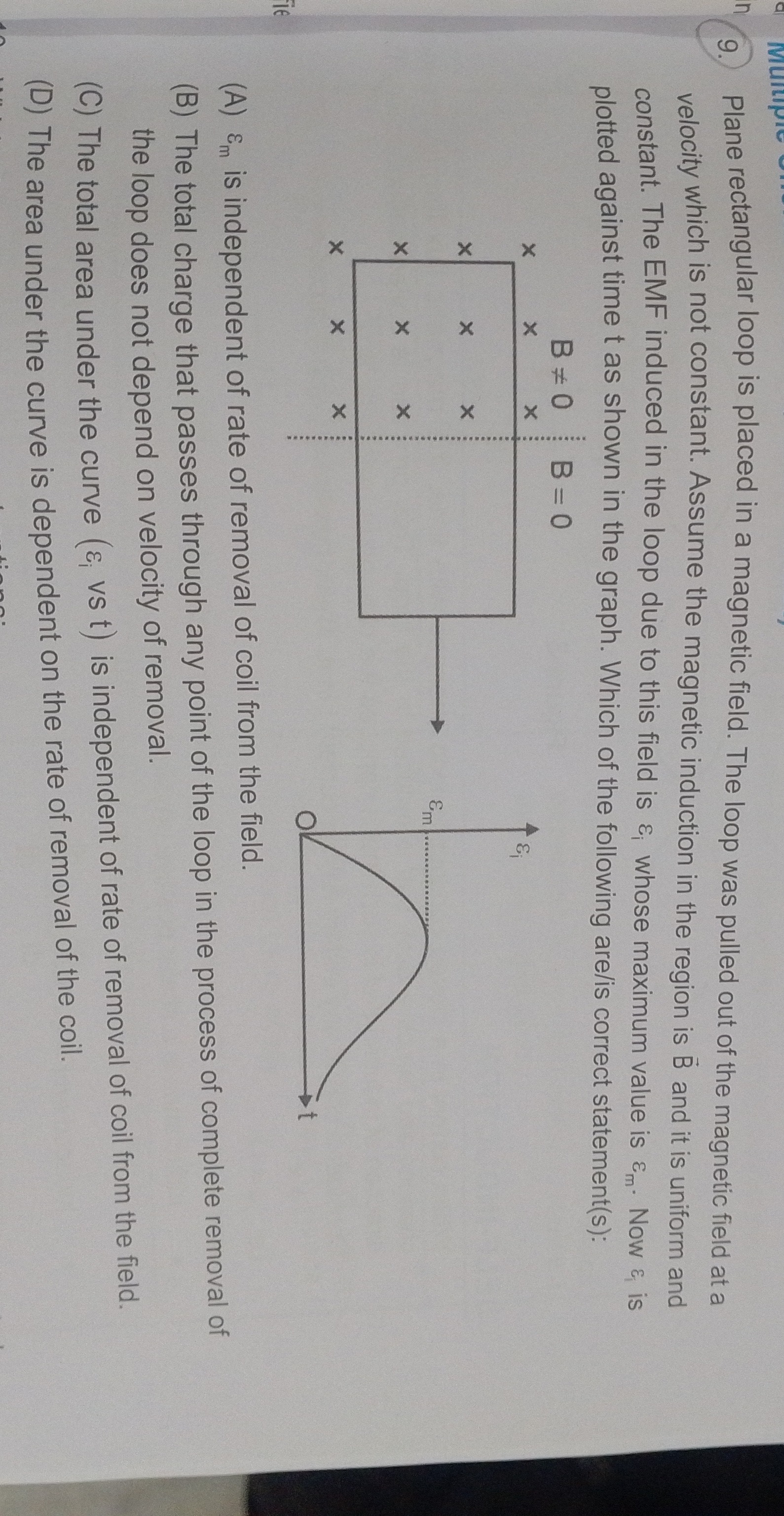
• A. $\varepsilon_m$ is independent of rate of removal of coil from the field.
• B. The total charge that passes through any point of the loop in the process of complete removal of the loop does not depend on velocity of removal.
• C. The total area under the curve ($\varepsilon_i$ vs t) is independent of rate of removal of coil from the field.
• D. The area under the curve is dependent on the rate of removal of the coil.

Answer 1

Answer: (B), (C)

Options (B) and (C) are correct.

Answer 2

The problem involves a rectangular loop being pulled out of a uniform and constant magnetic field. We need to analyze the induced EMF ($\varepsilon_i$), its maximum value ($\varepsilon_m$), the total charge ($Q$), and the area under the $\varepsilon_i$ vs. time graph.

Let the width of the loop (the side perpendicular to the velocity and magnetic field) be $l$, and the length of the loop (the side parallel to the velocity) be $w$. The magnetic field strength is $B$. The resistance of the loop is $R$.

1. Induced EMF: According to Faraday's Law of Electromagnetic Induction, the induced EMF is given by: $\varepsilon_i = -\frac{d\Phi_B}{dt}$ where $\Phi_B$ is the magnetic flux through the loop. When the loop is pulled out of the field, the area inside the field changes. If the velocity of the loop is $v$, the rate of change of area is $l v$. So, the magnitude of the induced EMF is $\varepsilon_i = Blv$.

2. Analysis of Options:

   (A) $\varepsilon_m$ is independent of rate of removal of coil from the field. The maximum EMF, $\varepsilon_m$, occurs when the velocity is maximum, $v_{max}$. So, $\varepsilon_m = Blv_{max}$. The "rate of removal" refers to the velocity of the coil. If the coil is removed at a higher rate, $v_{max}$ will be higher, and consequently, $\varepsilon_m$ will be higher. Therefore, $\varepsilon_m$ is dependent on the rate of removal. Statement (A) is incorrect.

   (B) The total charge that passes through any point of the loop in the process of complete removal of the loop does not depend on velocity of removal. The induced current is $I = \frac{\varepsilon_i}{R}$. The total charge $Q$ is the integral of current over time: $Q = \int I dt = \int \frac{\varepsilon_i}{R} dt$ Substituting $\varepsilon_i = -\frac{d\Phi_B}{dt}$: $Q = \int \frac{1}{R} \left(-\frac{d\Phi_B}{dt}\right) dt = -\frac{1}{R} \int d\Phi_B = -\frac{1}{R} [\Phi_B]_{initial}^{final}$ Initially, the loop is completely inside the magnetic field, so the flux is $\Phi_{initial} = B \cdot (\text{Area of loop}) = Blw$. Finally, the loop is completely out of the magnetic field, so the flux is $\Phi_{final} = 0$. The change in flux is $\Delta\Phi_B = \Phi_{final} - \Phi_{initial} = 0 - Blw = -Blw$. Therefore, the magnitude of the total charge is $|Q| = \frac{|-Blw|}{R} = \frac{Blw}{R}$. This expression for $Q$ depends only on $B$, $l$, $w$, and $R$, which are constants for the given setup. It does not depend on the velocity profile (how fast or slow the loop is removed). Statement (B) is correct.

   (C) The total area under the curve ($\varepsilon_i$ vs t) is independent of rate of removal of coil from the field. The area under the $\varepsilon_i$ vs t curve is given by $\int \varepsilon_i dt$. From Faraday's Law, $\int \varepsilon_i dt = \int \left(-\frac{d\Phi_B}{dt}\right) dt = -\int d\Phi_B = -[\Phi_B]_{initial}^{final}$. As calculated in option (B), the change in flux is $\Delta\Phi_B = -Blw$. So, the area under the curve is $-(-Blw) = Blw$. This area $Blw$ depends only on the magnetic field strength and the dimensions of the loop. It does not depend on the velocity profile (rate of removal). Statement (C) is correct.

   (D) The area under the curve is dependent on the rate of removal of the coil. This statement contradicts statement (C). Since (C) is correct, (D) must be incorrect.

Based on the analysis, statements (B) and (C) are correct.