Solveeit Logo
Login

Question

Question: Let x be a positive real number. Then the infinite sum $\sum_{n=1}^{\infty} \frac{(n-1)!}{(x+1)(x+2)...

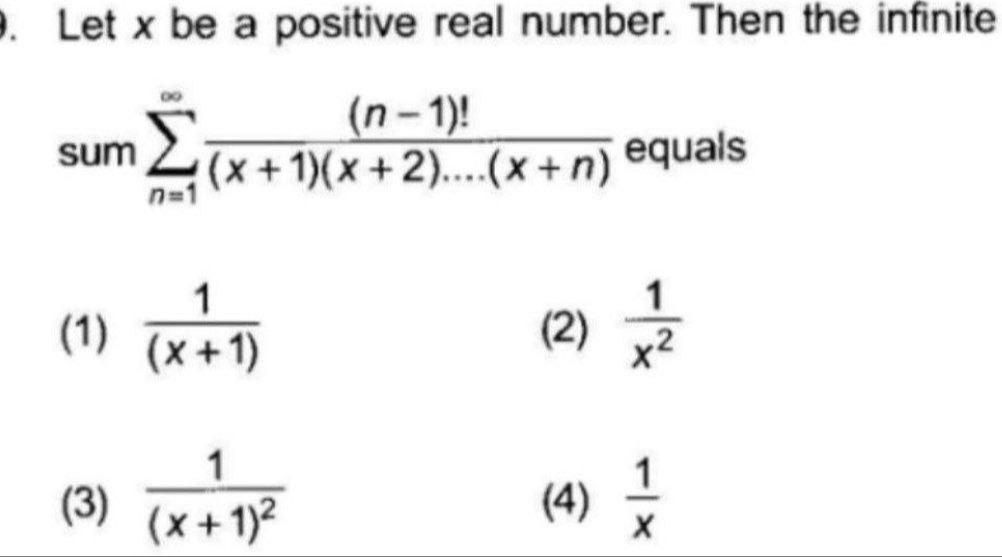
Let x be a positive real number. Then the infinite sum ∑n=1∞(n−1)!(x+1)(x+2)...(x+n)\sum_{n=1}^{\infty} \frac{(n-1)!}{(x+1)(x+2)...(x+n)} equals

A

1(x+1)\frac{1}{(x+1)}

B

1x2\frac{1}{x^2}

C

1(x+1)2\frac{1}{(x+1)^2}

D

1x\frac{1}{x}

Answer

1x\frac{1}{x}

Explanation

Solution

The general term of the series can be written as an=(n−1)!Γ(x+1)Γ(x+n+1)a_n = \frac{(n-1)! \Gamma(x+1)}{\Gamma(x+n+1)}, which is the Beta function B(n,x+1)B(n, x+1). Using the integral representation of the Beta function, an=∫01tn−1(1−t)xdta_n = \int_0^1 t^{n-1} (1-t)^x dt. The sum of the series is S=∑n=1∞∫01tn−1(1−t)xdtS = \sum_{n=1}^{\infty} \int_0^1 t^{n-1} (1-t)^x dt. Interchanging summation and integration, we get S=∫01∑n=1∞tn−1(1−t)xdtS = \int_0^1 \sum_{n=1}^{\infty} t^{n-1} (1-t)^x dt. The sum is a geometric series: ∑n=1∞tn−1=11−t\sum_{n=1}^{\infty} t^{n-1} = \frac{1}{1-t} for ∣t∣<1|t|<1. Thus, S=∫0111−t(1−t)xdt=∫01(1−t)x−1dtS = \int_0^1 \frac{1}{1-t} (1-t)^x dt = \int_0^1 (1-t)^{x-1} dt. Evaluating this integral gives S=[(1−t)x−x]01S = \left[ \frac{(1-t)^x}{-x} \right]_0^1, which is incorrect. Using substitution u=1−tu=1-t, du=−dtdu=-dt, the integral becomes ∫10ux−1(−du)=∫01ux−1du=[uxx]01=1xx−0xx=1x\int_1^0 u^{x-1} (-du) = \int_0^1 u^{x-1} du = \left[ \frac{u^x}{x} \right]_0^1 = \frac{1^x}{x} - \frac{0^x}{x} = \frac{1}{x} (since x>0x>0).