Question

Let $g(x)$ be a function defined on $R$ such that $g'(x) = g'(5050 - x) \forall x \in [0, 5050]$. If $g(0) = 1$ and $g(5050) = 100$ and $\int_{0}^{5050} g(x) dx = k(5050)$ then k equals

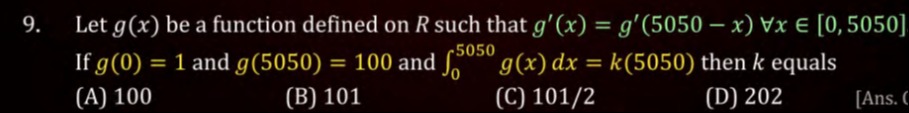
• A. 100
• B. 101
• C. 101/2
• D. 202

Answer 1

Answer: (C)

101/2

Answer 2

Let $a = 5050$. The given condition is $g'(x) = g'(a - x)$ for $x \in [0, a]$. Integrating both sides with respect to $x$, we get: $\int g'(x) dx = \int g'(a - x) dx$ $g(x) = -g(a - x) + C$ $g(x) + g(a - x) = C$

Using the given values $g(0) = 1$ and $g(a) = 100$: For $x=0$, $g(0) + g(a - 0) = C \implies 1 + 100 = C \implies C = 101$. Thus, $g(x) + g(a - x) = 101$ for $x \in [0, a]$.

Let the integral be $I = \int_{0}^{a} g(x) dx$. We are given $I = k \cdot a$. Using the property $\int_{0}^{a} f(x) dx = \int_{0}^{a} f(a - x) dx$: $I = \int_{0}^{a} g(a - x) dx$.

Adding the two expressions for $I$: $2I = \int_{0}^{a} g(x) dx + \int_{0}^{a} g(a - x) dx$ $2I = \int_{0}^{a} [g(x) + g(a - x)] dx$

Substitute $g(x) + g(a - x) = 101$: $2I = \int_{0}^{a} 101 dx$ $2I = 101 [x]_{0}^{a}$ $2I = 101 (a - 0)$ $2I = 101a$

Given $I = ka$: $2(ka) = 101a$ $2k = 101$ $k = \frac{101}{2}$