Question
Question: Let $f(x) = 2x^3 + ax^2 + bx - 3\cos^2 x$ then $f(x)$ is an increasing function for all $x \in R$ if...
Let f(x)=2x3+ax2+bx−3cos2x then f(x) is an increasing function for all x∈R if
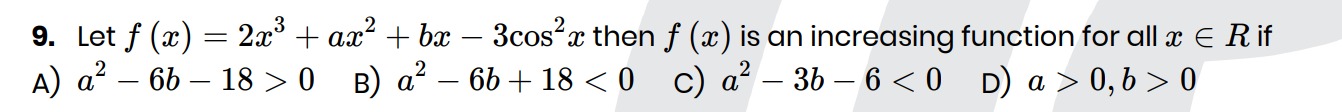
a2−6b−18>0
a2−6b+18<0
a2−3b−6<0
a>0,b>0
B
Solution
For a function f(x) to be an increasing function for all x∈R, its derivative f′(x) must be greater than or equal to zero for all x∈R.
Given the function f(x)=2x3+ax2+bx−3cos2x.
First, let's find the derivative f′(x): f′(x)=dxd(2x3)+dxd(ax2)+dxd(bx)−dxd(3cos2x)
- dxd(2x3)=6x2
- dxd(ax2)=2ax
- dxd(bx)=b
- For −3cos2x, we use the chain rule: dxd(−3cos2x)=−3⋅2cosx⋅(−sinx) =6sinxcosx Using the identity sin(2x)=2sinxcosx, we get: =3(2sinxcosx)=3sin(2x)
So, f′(x)=6x2+2ax+b+3sin(2x).
For f(x) to be an increasing function for all x∈R, we must have f′(x)≥0 for all x∈R. 6x2+2ax+b+3sin(2x)≥0 for all x∈R.
Let's rearrange the inequality: 6x2+2ax+b≥−3sin(2x).
For this inequality to hold for all x∈R, the minimum value of the quadratic expression on the left-hand side must be greater than or equal to the maximum value of the trigonometric expression on the right-hand side.
-
Minimum value of the quadratic P(x)=6x2+2ax+b: This is a parabola opening upwards (A=6>0). Its minimum value occurs at x=−2(6)2a=−6a. The minimum value is P(−6a)=6(−6a)2+2a(−6a)+b =6(36a2)−62a2+b =6a2−3a2+b =6a2−2a2+b =−6a2+b Alternatively, using the formula for the minimum value of Ax2+Bx+C which is 4A4AC−B2: Pmin=4(6)4(6)(b)−(2a)2=2424b−4a2=b−6a2.
-
Maximum value of −3sin(2x): We know that −1≤sin(2x)≤1. Multiplying by −3 (and reversing the inequality signs): −3≤−3sin(2x)≤3. So, the maximum value of −3sin(2x) is 3.
For 6x2+2ax+b≥−3sin(2x) to hold for all x, we must have: min(6x2+2ax+b)≥max(−3sin(2x)) b−6a2≥3
Multiply by 6 to clear the denominator: 6b−a2≥18
Rearrange the terms to match the options: −a2+6b−18≥0 a2−6b+18≤0
Comparing this with the given options: A) a2−6b−18>0 B) a2−6b+18<0 C) a2−3b−6<0 D) a>0,b>0
Our derived condition is a2−6b+18≤0. Option B is a2−6b+18<0. Since f′(x)≥0 is the condition for an increasing function, a2−6b+18≤0 is the correct condition. If the options contain a strict inequality, it usually implies that the function is strictly increasing, or that the problem expects a slightly stronger condition. In competitive exams, if ≤ is derived and < is an option, it's often the intended answer, implying that equality might lead to points where f′(x)=0 over an interval, which is not strictly increasing. However, for "increasing function", f′(x)≥0 is the standard definition. Given the options, a2−6b+18<0 is the closest match and represents a sufficient condition for f′(x)>0 everywhere, which implies f(x) is strictly increasing, and thus also increasing.
