Question

In the system shown, mass $m$ is resting on a rough horizontal surface ($\mu = 3/4$). Mass $M$ is held in such a way that the spring is at its natural length. Find the minimum value of $M$ required to move the block up the plane. (Neglect mass of string and pulley. Ignore friction in pulley).

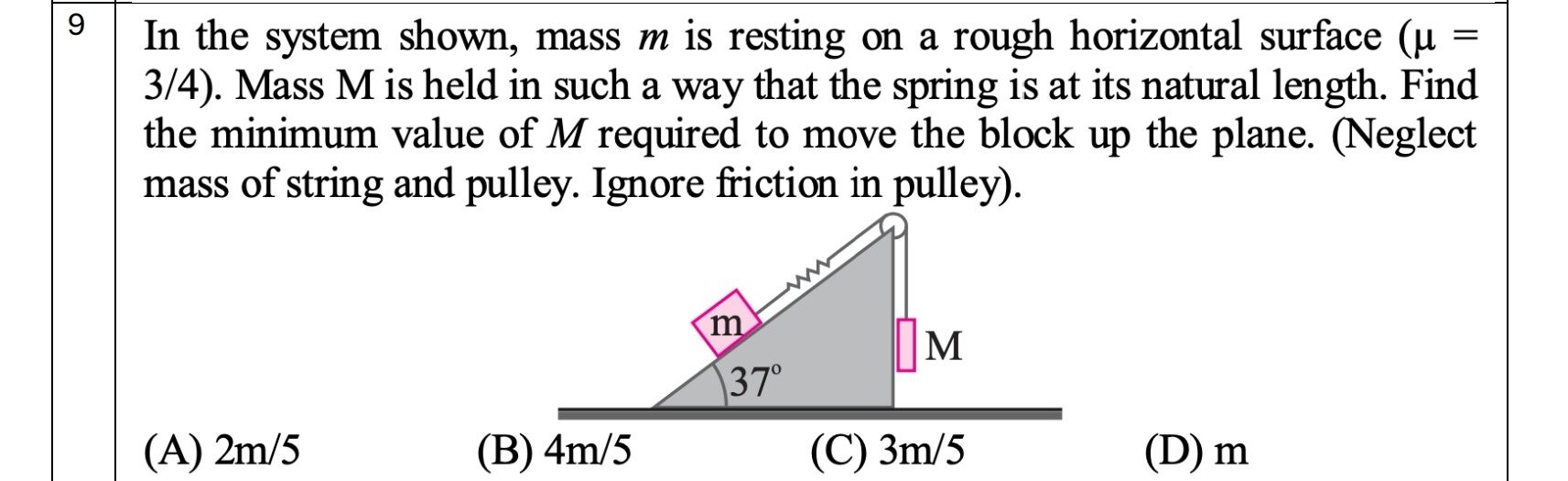
• A. 2m/5
• B. 4m/5
• C. 3m/5
• D. m

Answer 1

None of the above. The correct answer is 6m/5

Answer 2

The problem asks for the minimum value of mass $M$ required to move the block $m$ up the inclined plane.

Forces acting on mass $m$ (on the inclined plane):

• Gravity ($mg$): Acts vertically downwards. We resolve it into components parallel and perpendicular to the incline.
  • Component perpendicular to the incline: $mg \cos(37^\circ)$.
  • Component parallel to the incline (down the plane): $mg \sin(37^\circ)$.
• Normal force ($N$): Acts perpendicular to the incline, upwards.
• Friction force ($f_s$): Since the block is on the verge of moving up the plane, the friction force opposes this motion and acts down the plane. Its maximum value is $f_s = \mu N$.
• Tension ($T$): From the string, acting up the plane.
• Spring force ($F_s$): The problem states the spring is at its natural length initially. For the block to start moving, it hasn't moved yet, so the spring's extension is zero. Therefore, the spring force $F_s = 0$ at the instant motion begins.

Values for trigonometric functions: For $37^\circ$, we use the common approximations: $\sin(37^\circ) = 3/5$ $\cos(37^\circ) = 4/5$

Equilibrium perpendicular to the incline for mass $m$: The block is not accelerating perpendicular to the plane. $N = mg \cos(37^\circ)$ $N = mg (4/5)$

Maximum static friction: $f_s = \mu N = (3/4) \times (4/5)mg = (3/5)mg$

Equilibrium parallel to the incline for mass $m$ (on the verge of moving up): The sum of forces parallel to the incline is zero for impending motion. Forces acting down the plane: $mg \sin(37^\circ)$ and $f_s$. Force acting up the plane: $T$. Since the spring force is zero at the onset of motion: $T = mg \sin(37^\circ) + f_s$ $T = mg (3/5) + (3/5)mg$ $T = (6/5)mg$

Forces acting on mass $M$ (hanging vertically):

• Gravity ($Mg$): Acts downwards.
• Tension ($T$): Acts upwards.

Equilibrium for mass $M$ (on the verge of moving down): The sum of vertical forces is zero for impending motion. $Mg = T$

Combining the equations: Substitute the expression for $T$ from the forces on mass $m$: $Mg = (6/5)mg$ $M = (6/5)m$