Question

In the figure shown the velocity of lift is 2 m/s while string is winding on the motor shaft with velocity 2 m/s and block A is moving downwards with a velocity of 2 m/s, then find out the velocity of block B

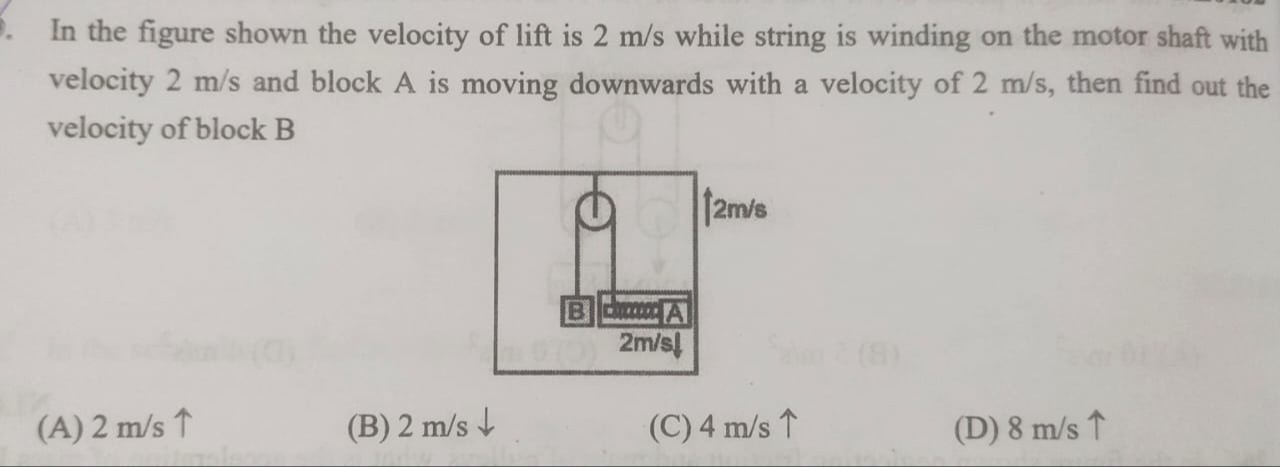
• A. 2 m/s ↑
• B. 2 m/s↓
• C. 4 m/s ↑
• D. 8 m/s ↑

Answer 1

Answer: (D)

8 m/s ↑

Answer 2

To determine the velocity of block B, we will use the concept of relative velocities and the constraint equation for the string-pulley system.

Let's define our coordinate system: Upwards is positive (+), and downwards is negative (-).

Given information:

1. Velocity of the lift ($V_L$): 2 m/s upwards. So, $V_L = +2$ m/s.
2. Velocity of the pulley ($V_P$): Since the pulley is fixed to the lift, its velocity is the same as the lift's velocity. So, $V_P = V_L = +2$ m/s.
3. Velocity of block A ($V_A$): 2 m/s downwards. So, $V_A = -2$ m/s.
4. String winding on motor shaft: The string is winding on the motor shaft with a velocity of 2 m/s. This means the total active length of the string (the part of the string that is free to move over the pulley and connected to the blocks) is decreasing at a rate of 2 m/s. Let this rate of change of active string length be $dL_{active}/dt$. Since the length is decreasing, $dL_{active}/dt = -2$ m/s.

Consider the active length of the string. Let $y_P$ be the position of the pulley, $y_A$ be the position of block A, and $y_B$ be the position of block B, all measured from a fixed ground reference. The length of the string segment from the pulley to block A is $(y_P - y_A)$. The length of the string segment from the pulley to block B is $(y_P - y_B)$. The total active length of the string, $L_{active}$, is the sum of these two segments: $L_{active} = (y_P - y_A) + (y_P - y_B)$ $L_{active} = 2y_P - y_A - y_B$

Now, we differentiate this equation with respect to time to find the relationship between the velocities: $\frac{dL_{active}}{dt} = \frac{d}{dt}(2y_P - y_A - y_B)$ $\frac{dL_{active}}{dt} = 2\frac{dy_P}{dt} - \frac{dy_A}{dt} - \frac{dy_B}{dt}$ Substituting the velocities ($V = dy/dt$): $\frac{dL_{active}}{dt} = 2V_P - V_A - V_B$

Now, substitute the known values into this equation: $-2 \text{ m/s} = 2(+2 \text{ m/s}) - (-2 \text{ m/s}) - V_B$ $-2 = 4 + 2 - V_B$ $-2 = 6 - V_B$

Now, solve for $V_B$: $V_B = 6 + 2$ $V_B = 8$ m/s

Since the value of $V_B$ is positive, block B is moving upwards. Therefore, the velocity of block B is 8 m/s upwards.