Question

If $x = \log_{2a} a$, $y = \log_{3a} 2a$ and $z = \log_{4a} 3a$, prove that: $xyz + 1 = 2yz$.

Answer 1

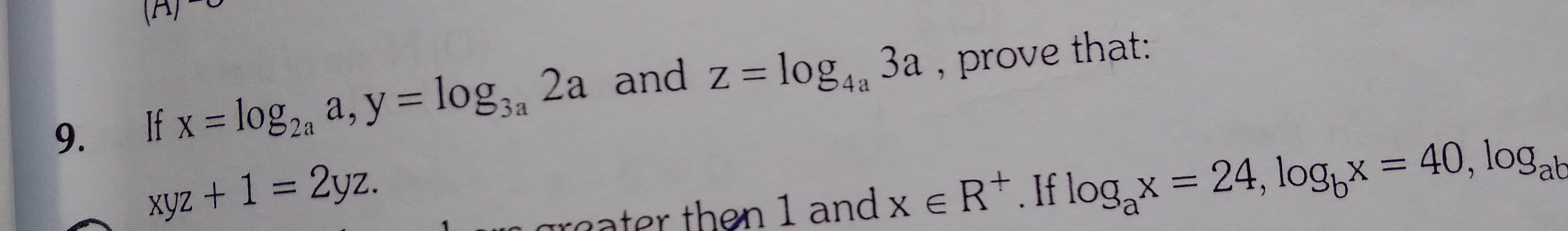
The identity $xyz + 1 = 2yz$ is proven to be true.

Answer 2

We use the change of base formula for logarithms: $\log_b c = \frac{\log_k c}{\log_k b}$. Let's convert all logarithms to base $a$.

Given: $x = \log_{2a} a$ Using the change of base formula with base $a$: $x = \frac{\log_a a}{\log_a 2a} = \frac{1}{\log_a 2a}$ This implies: $\log_a 2a = \frac{1}{x}$ (Equation 1)

$y = \log_{3a} 2a$ Using the change of base formula with base $a$: $y = \frac{\log_a 2a}{\log_a 3a}$ Substitute the expression for $\log_a 2a$ from Equation 1: $y = \frac{1/x}{\log_a 3a}$ This implies: $\log_a 3a = \frac{1}{xy}$ (Equation 2)

$z = \log_{4a} 3a$ Using the change of base formula with base $a$: $z = \frac{\log_a 3a}{\log_a 4a}$ Substitute the expression for $\log_a 3a$ from Equation 2: $z = \frac{1/(xy)}{\log_a 4a}$ This implies: $\log_a 4a = \frac{1}{xyz}$ (Equation 3)

Now, we expand the terms in Equations 1, 2, and 3 using the logarithm properties $\log(AB) = \log A + \log B$.

From Equation 1: $\log_a 2a = \log_a 2 + \log_a a = \log_a 2 + 1$ So, $\log_a 2 + 1 = \frac{1}{x}$ This gives us: $\log_a 2 = \frac{1}{x} - 1$ (Equation 4)

From Equation 3: $\log_a 4a = \log_a 4 + \log_a a = \log_a 2^2 + 1 = 2 \log_a 2 + 1$ So, $2 \log_a 2 + 1 = \frac{1}{xyz}$ (Equation 5)

Now, substitute the expression for $\log_a 2$ from Equation 4 into Equation 5: $2 \left(\frac{1}{x} - 1\right) + 1 = \frac{1}{xyz}$ $\frac{2}{x} - 2 + 1 = \frac{1}{xyz}$ $\frac{2}{x} - 1 = \frac{1}{xyz}$

Multiply both sides by $xyz$: $xyz \left(\frac{2}{x} - 1\right) = xyz \left(\frac{1}{xyz}\right)$ $2yz - xyz = 1$ Rearranging this equation gives: $xyz + 1 = 2yz$

This proves the given identity.