Solveeit Logo
Login

Question

Question: If the area of a triangle whose vertices are (2a, b), (a + b, 2b + a), (2b, 2a) be $\lambda$ then th...

If the area of a triangle whose vertices are (2a, b), (a + b, 2b + a), (2b, 2a) be λ\lambda then the area of the triangle whose vertices are (a + b, a - b), (3b - a, b + 3a) and (3a – b, 3b – a) is

A

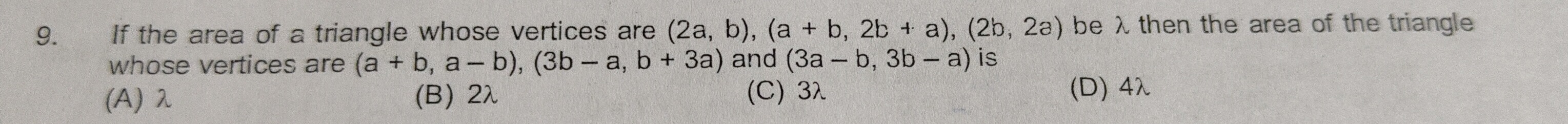
λ\lambda

B

2λ2\lambda

C

3λ3\lambda

D

4λ4\lambda

Answer

4λ\lambda

Explanation

Solution

The area of a triangle with vertices (x1,y1)(x_1, y_1), (x2,y2)(x_2, y_2), and (x3,y3)(x_3, y_3) is given by the formula: Area =12∣x1(y2−y3)+x2(y3−y1)+x3(y1−y2)∣= \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|

For the first triangle with vertices A=(2a,b)A = (2a, b), B=(a+b,a+2b)B = (a + b, a + 2b), and C=(2b,2a)C = (2b, 2a): x1=2a,y1=bx_1 = 2a, y_1 = b x2=a+b,y2=a+2bx_2 = a + b, y_2 = a + 2b x3=2b,y3=2ax_3 = 2b, y_3 = 2a

Calculating the area λ\lambda: λ=12∣2a((a+2b)−2a)+(a+b)(2a−b)+2b(b−(a+2b))∣\lambda = \frac{1}{2} |2a((a + 2b) - 2a) + (a + b)(2a - b) + 2b(b - (a + 2b))| λ=12∣2a(2b−a)+(2a2−ab+2ab−b2)+2b(−a−b)∣\lambda = \frac{1}{2} |2a(2b - a) + (2a^2 - ab + 2ab - b^2) + 2b(-a - b)| λ=12∣4ab−2a2+2a2+ab−b2−2ab−2b2∣\lambda = \frac{1}{2} |4ab - 2a^2 + 2a^2 + ab - b^2 - 2ab - 2b^2| λ=12∣3ab−3b2∣\lambda = \frac{1}{2} |3ab - 3b^2| λ=32∣ab−b2∣\lambda = \frac{3}{2} |ab - b^2|

For the second triangle with vertices P=(a+b,a−b)P = (a + b, a - b), Q=(3b−a,b+3a)Q = (3b - a, b + 3a), and R=(3a–b,3b–a)R = (3a – b, 3b – a): x1′=a+b,y1′=a−bx'_1 = a + b, y'_1 = a - b x2′=3b−a,y2′=b+3ax'_2 = 3b - a, y'_2 = b + 3a x3′=3a−b,y3′=3b−ax'_3 = 3a - b, y'_3 = 3b - a

Calculating the area of the second triangle: Area =12∣(a+b)((b+3a)−(3b−a))+(3b−a)((3b−a)−(a−b))+(3a−b)((a−b)−(b+3a))∣= \frac{1}{2} |(a + b)((b + 3a) - (3b - a)) + (3b - a)((3b - a) - (a - b)) + (3a - b)((a - b) - (b + 3a))| Area =12∣(a+b)(4a−2b)+(3b−a)(4b−2a)+(3a−b)(−2a−2b)∣= \frac{1}{2} |(a + b)(4a - 2b) + (3b - a)(4b - 2a) + (3a - b)(-2a - 2b)| Area =12∣(4a2−2ab+4ab−2b2)+(12b2−6ab−4ab+2a2)+(−6a2−6ab+2ab+2b2)∣= \frac{1}{2} |(4a^2 - 2ab + 4ab - 2b^2) + (12b^2 - 6ab - 4ab + 2a^2) + (-6a^2 - 6ab + 2ab + 2b^2)| Area =12∣(4a2+2ab−2b2)+(2a2−10ab+12b2)+(−6a2−4ab+2b2)∣= \frac{1}{2} |(4a^2 + 2ab - 2b^2) + (2a^2 - 10ab + 12b^2) + (-6a^2 - 4ab + 2b^2)| Area =12∣(4+2−6)a2+(2−10−4)ab+(−2+12+2)b2∣= \frac{1}{2} |(4+2-6)a^2 + (2-10-4)ab + (-2+12+2)b^2| Area =12∣0a2−12ab+12b2∣= \frac{1}{2} |0a^2 - 12ab + 12b^2| Area =12∣−12ab+12b2∣= \frac{1}{2} |-12ab + 12b^2| Area =6∣b2−ab∣= 6 |b^2 - ab| Since ∣b2−ab∣=∣−(ab−b2)∣=∣ab−b2∣|b^2 - ab| = |-(ab - b^2)| = |ab - b^2|, the area is 6∣ab−b2∣6 |ab - b^2|.

From the first triangle, we have λ=32∣ab−b2∣\lambda = \frac{3}{2} |ab - b^2|. Therefore, ∣ab−b2∣=23λ|ab - b^2| = \frac{2}{3}\lambda.

Substituting this into the area of the second triangle: Area =6×(23λ)=4λ= 6 \times \left(\frac{2}{3}\lambda\right) = 4\lambda.