Question
Question: If $\sum_{r=0}^{2n} a_r (x-2)^r = \sum_{r=0}^{2n} b_r (x-3)^r$ and $a_k = 1 \ \forall k \ge n$, show...
If ∑r=02nar(x−2)r=∑r=02nbr(x−3)r and ak=1 ∀k≥n, show that bn=2n+1Cn+1.
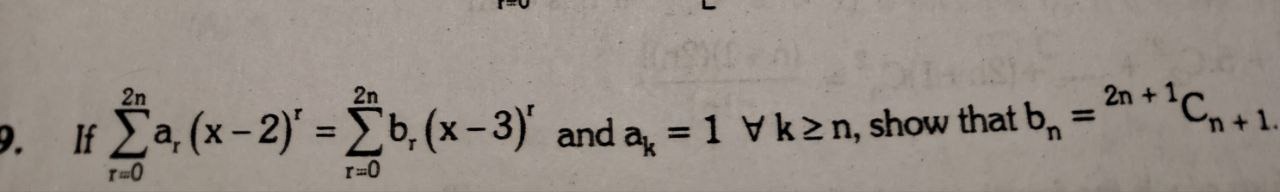
^{2n+1}C_{n+1}
Solution
The problem asks us to show that bn=2n+1Cn+1, given two series expansions of a polynomial P(x) and a condition on the coefficients ak.
Let the given polynomial be P(x). We have two representations for P(x):
- P(x)=∑r=02nar(x−2)r
- P(x)=∑r=02nbr(x−3)r
We are given that ak=1 for all k≥n. We need to find the coefficient bn.
From the second representation, P(x)=∑r=02nbr(x−3)r, we know that bn is the coefficient of (x−3)n. According to Taylor's theorem, the coefficient bn is given by: bn=n!P(n)(3)
Now, let's use the first representation of P(x) to find its n-th derivative and evaluate it at x=3. P(x)=∑r=02nar(x−2)r
We can split the sum based on the given condition ak=1 for k≥n: P(x)=∑r=0n−1ar(x−2)r+∑r=n2nar(x−2)r Since ar=1 for r≥n: P(x)=∑r=0n−1ar(x−2)r+∑r=n2n(x−2)r
Now, we need to find the n-th derivative of P(x), P(n)(x). Consider the terms in the first sum: ∑r=0n−1ar(x−2)r. If r<n, then the n-th derivative of (x−2)r will be zero. For example, dxndn(x−2)0=0, dxndn(x−2)1=0, ..., dxndn(x−2)n−1=0. So, the first sum contributes zero to P(n)(x).
Thus, P(n)(x) is determined solely by the second sum: P(n)(x)=dxndn(∑r=n2n(x−2)r) P(n)(x)=∑r=n2ndxndn(x−2)r
The n-th derivative of (x−c)r is given by (r−n)!r!(x−c)r−n. So, for (x−2)r: dxndn(x−2)r=(r−n)!r!(x−2)r−n
Substituting this back into P(n)(x): P(n)(x)=∑r=n2n(r−n)!r!(x−2)r−n
Now, evaluate P(n)(x) at x=3: P(n)(3)=∑r=n2n(r−n)!r!(3−2)r−n P(n)(3)=∑r=n2n(r−n)!r!(1)r−n P(n)(3)=∑r=n2n(r−n)!r!
Finally, substitute this into the formula for bn: bn=n!P(n)(3)=n!1∑r=n2n(r−n)!r! bn=∑r=n2nn!(r−n)!r! Recognizing the definition of a binomial coefficient (kn)=k!(n−k)!n!: bn=∑r=n2n(nr)
This sum is a known binomial identity, often called the Hockey-stick identity or Christmas stocking identity: ∑k=rm(rk)=(r+1m+1) In our case, the summation variable is r, the lower index of the binomial coefficient is n, and the upper limit of the summation is 2n. Applying the identity: bn=(n+12n+1)
Thus, we have shown that bn=2n+1Cn+1.
