Question

Heat produced is In the figure shown a rod is kept on floor and applied some forces. The area of cross-section is A and Young's modulus is Y (Assume all forces are applied uniformly distributed throughout cross section of rod)

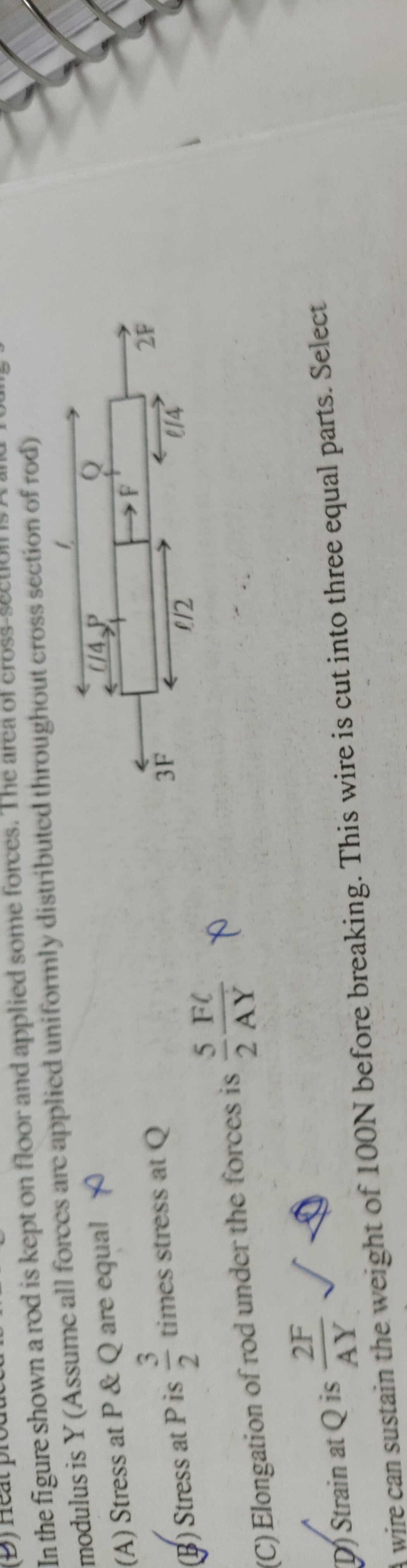
• A. Stress at P & Q are equal
• B. Stress at P is $\frac{3}{2}$ times stress at Q
• C. Elongation of rod under the forces is $\frac{5Fl}{2AY}$
• D. Strain at Q is $\frac{2F}{AY}$

Answer 1

Answer: (A), (C)

A, C

Answer 2

The problem describes a rod with cross-sectional area $A$ and Young's modulus $Y$, subjected to various forces. We need to evaluate the given statements.

Let's assume the forces $3F$ and $2F$ are axial forces applied along the length of the rod. Consider the internal axial force $N(x)$ at a distance $x$ from the left end.

For the segment $0 \le x < l/2$: The force applied at the left end is $3F$ downwards. For equilibrium, the internal axial force in this segment must be $N(x) = 3F$ (tension). The stress in this region is $\sigma(x) = N(x)/A = 3F/A$. Point P is at $x = l/4$, so the stress at P is $\sigma_P = 3F/A$. Point Q is at $x = l/2$, so the stress at Q is $\sigma_Q = 3F/A$.

Statement (A): Stress at P & Q are equal. Since $\sigma_P = 3F/A$ and $\sigma_Q = 3F/A$, this statement is correct.

Statement (B): Stress at P is $\frac{3}{2}$ times stress at Q. Since $\sigma_P = \sigma_Q$, this statement is incorrect.

Now, let's consider the elongation of the rod. The total elongation is given by $\Delta l = \int_0^l \epsilon(x) dx = \int_0^l \frac{\sigma(x)}{Y} dx$.

For the segment $0 \le x < l/2$, $\sigma(x) = 3F/A$. The elongation of this segment is: $\Delta l_1 = \int_0^{l/2} \frac{3F}{AY} dx = \frac{3F}{AY} \left[x\right]_0^{l/2} = \frac{3F}{AY} \left(\frac{l}{2}\right) = \frac{3Fl}{2AY}$.

For the segment $l/2 \le x \le l$: We assume that the internal axial force in this segment is $2F$ (tension), consistent with the calculation for option (C). The stress in this region is $\sigma(x) = 2F/A$. The elongation of this segment is: $\Delta l_2 = \int_{l/2}^l \frac{2F}{AY} dx = \frac{2F}{AY} \left[x\right]_{l/2}^l = \frac{2F}{AY} \left(l - \frac{l}{2}\right) = \frac{2F}{AY} \left(\frac{l}{2}\right) = \frac{Fl}{AY}$.

The total elongation of the rod is $\Delta l = \Delta l_1 + \Delta l_2 = \frac{3Fl}{2AY} + \frac{Fl}{AY} = \frac{3Fl + 2Fl}{2AY} = \frac{5Fl}{2AY}$.

Statement (C): Elongation of rod under the forces is $\frac{5Fl}{2AY}$. Based on our calculation, this statement is correct.

Statement (D): Strain at Q is $\frac{2F}{AY}$. The strain at Q is $\epsilon_Q = \sigma_Q/Y$. Since $\sigma_Q = 3F/A$, the strain at Q is $\epsilon_Q = \frac{3F}{AY}$. Therefore, this statement is incorrect.

Both statements (A) and (C) are correct.