Question

From the point (-1, 2) tangent lines are drawn to the parabola $y^2 = 4x$. If area of triangle formed by the chord of contact and the tangents is $N\sqrt{2}$, then N =

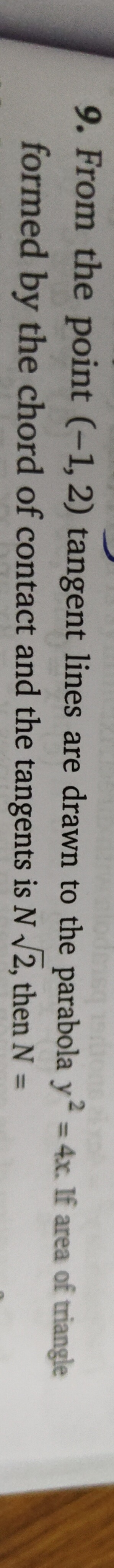
Answer 1

8

Answer 2

The equation of the parabola is $y^2 = 4x$, so $a=1$. The external point is $(x_1, y_1) = (-1, 2)$. The area of the triangle formed by the tangents from $(x_1, y_1)$ to the parabola $y^2 = 4ax$ and the chord of contact is given by $\frac{(y_1^2 - 4ax_1)^{3/2}}{2a}$. Substituting the values: Area $= \frac{((2)^2 - 4(1)(-1))^{3/2}}{2(1)}$ Area $= \frac{(4 + 4)^{3/2}}{2}$ Area $= \frac{(8)^{3/2}}{2}$ Area $= \frac{(\sqrt{8})^3}{2}$ Area $= \frac{(2\sqrt{2})^3}{2}$ Area $= \frac{16\sqrt{2}}{2}$ Area $= 8\sqrt{2}$ Given that the area is $N\sqrt{2}$, we have $N\sqrt{2} = 8\sqrt{2}$. Therefore, $N = 8$.