Question
Question: Find moment of inertia of a solid hemisphere of mass M shown in figure, about an axis AA' passing th...
Find moment of inertia of a solid hemisphere of mass M shown in figure, about an axis AA' passing through its centre of mass.
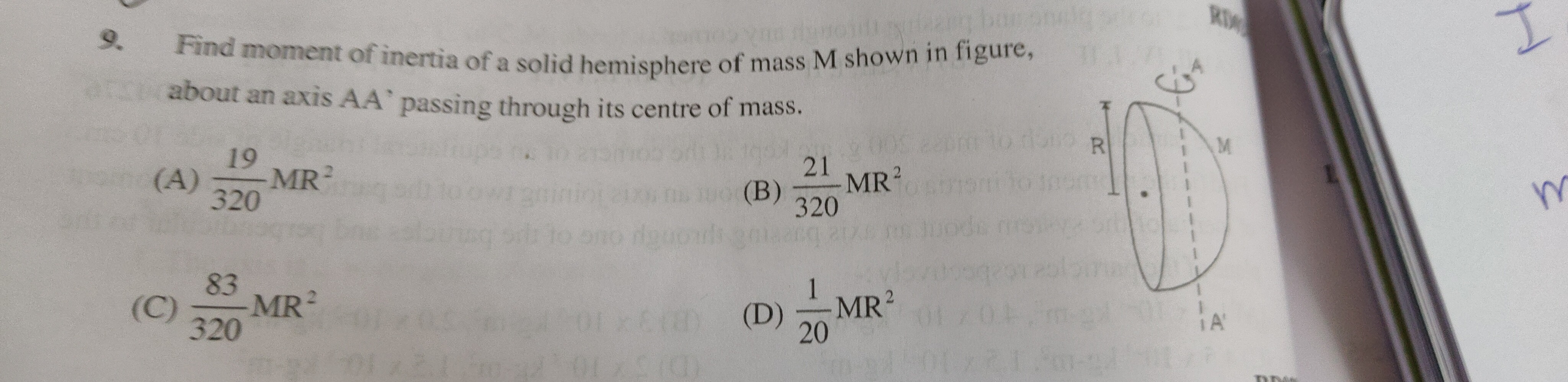
32019MR2
32021MR2
32083MR2
201MR2
(C)
Solution
-
Moment of Inertia of Solid Hemisphere about its Base:
The moment of inertia of a solid sphere of mass Msphere and radius R about its diameter is given by Isphere=52MsphereR2.
A solid hemisphere of mass M can be considered as half of a solid sphere of mass 2M.
Therefore, the moment of inertia of the solid hemisphere about an axis passing through the center of its flat base and perpendicular to the base (let's call this I0) is:
I0=21×(52(2M)R2)=52MR2
-
Center of Mass of Solid Hemisphere:
The center of mass (CM) of a solid hemisphere of radius R is located at a distance h=83R from its flat base, along the axis of symmetry. The axis AA' shown in the figure passes through this center of mass and is parallel to the axis I0.
-
Applying Parallel Axis Theorem:
The Parallel Axis Theorem states that I=ICM+Md2, where I is the moment of inertia about an axis, ICM is the moment of inertia about a parallel axis passing through the center of mass, M is the mass, and d is the perpendicular distance between the two parallel axes.
In our case, I=I0=52MR2, and the distance d between the axis through the base and the axis through the center of mass (AA') is h=83R.
So, we have:
I0=ICM+M(83R)2
52MR2=ICM+M(649R2)
-
Calculating ICM:
Now, solve for ICM:
ICM=52MR2−649MR2
To subtract the fractions, find a common denominator, which is 5×64=320:
ICM=(5×642×64−64×59×5)MR2
ICM=(320128−32045)MR2
ICM=(320128−45)MR2
ICM=32083MR2
The moment of inertia of the solid hemisphere about an axis AA' passing through its center of mass is 32083MR2.
