Question

Find area ericlosed by $y = \sin x, y = \cos^{-1}x, x$ - axis.

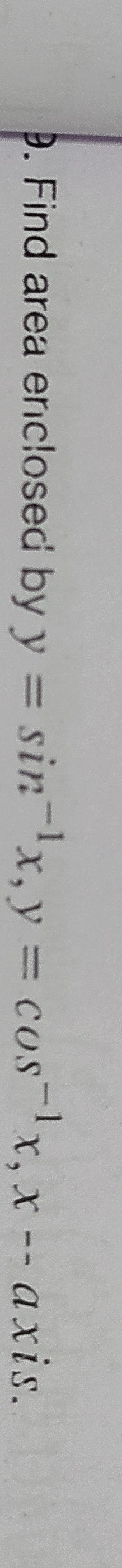
Answer 1

The area enclosed by $y = \sin x$, $y = \cos^{-1}x$, and the x-axis is given by: $A = 1 - \cos x_0 - x_0 \cos^{-1}x_0 + \sqrt{1-x_0^2}$ where $x_0$ is the unique solution to the equation $\sin x = \cos^{-1}x$.

Answer 2

The area is found by dividing the region into two parts: one under $y=\sin x$ from $x=0$ to the intersection point $x_0$, and the other under $y=\cos^{-1}x$ from $x_0$ to $x=1$. The intersection point $(x_0, y_0)$ is defined by $y_0 = \sin x_0 = \cos^{-1}x_0$. The integral of $\sin x$ is $-\cos x$, and the integral of $\cos^{-1}x$ is $x\cos^{-1}x - \sqrt{1-x^2}$. Evaluating these definite integrals and summing them yields the total area.