Question

Solve the equation $x^{2logx}=10x^2$. Assume $\log$ denotes the base-10 logarithm.

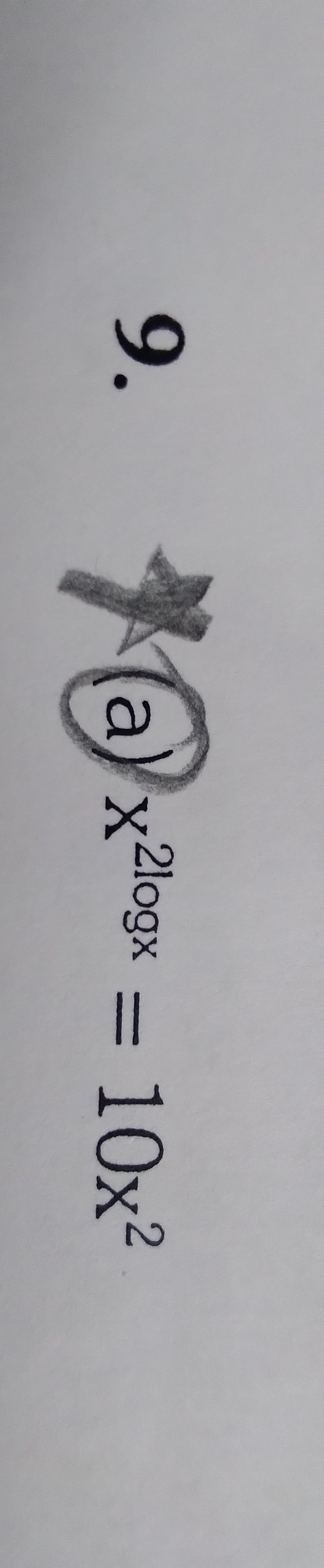
• A. Both $10^{\frac{1+\sqrt{3}}{2}}$ and $10^{\frac{1-\sqrt{3}}{2}}$
• B. $10^{\frac{1+\sqrt{3}}{2}}$
• C. $10^{\frac{1-\sqrt{3}}{2}}$
• D. $10$

Answer 1

Answer: (A)

Both $10^{\frac{1+\sqrt{3}}{2}}$ and $10^{\frac{1-\sqrt{3}}{2}}$

Answer 2

To solve the equation $x^{2\log x} = 10x^2$, we take the logarithm base 10 of both sides: $\log_{10}(x^{2\log_{10} x}) = \log_{10}(10x^2)$ Using logarithm properties: $(2\log_{10} x)(\log_{10} x) = \log_{10} 10 + \log_{10} x^2$ $2(\log_{10} x)^2 = 1 + 2\log_{10} x$ Let $y = \log_{10} x$. The equation becomes a quadratic: $2y^2 = 1 + 2y$ $2y^2 - 2y - 1 = 0$ Using the quadratic formula $y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$: $y = \frac{2 \pm \sqrt{(-2)^2 - 4(2)(-1)}}{2(2)} = \frac{2 \pm \sqrt{4 + 8}}{4} = \frac{2 \pm \sqrt{12}}{4} = \frac{2 \pm 2\sqrt{3}}{4} = \frac{1 \pm \sqrt{3}}{2}$ So, $\log_{10} x = \frac{1 + \sqrt{3}}{2}$ or $\log_{10} x = \frac{1 - \sqrt{3}}{2}$. Converting back to exponential form: $x = 10^{\frac{1 + \sqrt{3}}{2}} \quad \text{or} \quad x = 10^{\frac{1 - \sqrt{3}}{2}}$ Both solutions are positive and valid.