Question
Question: Co-efficient of $\alpha^t$ in the expansion of, $(\alpha + p)^{m-1} + (\alpha + p)^{m-2}(\alpha + q)...
Co-efficient of αt in the expansion of, (α+p)m−1+(α+p)m−2(α+q)+(α+p)m−3(α+q)2+......(α+q)m−1 where α=−q and p=q is:
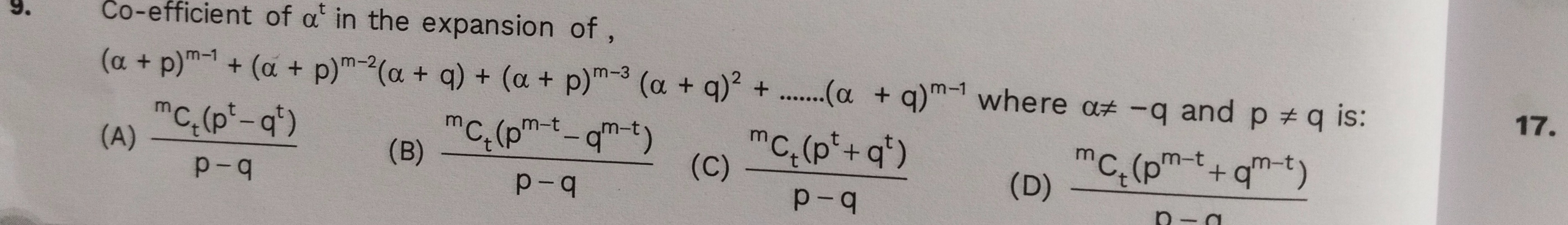
p−qmCt(pt−qt)
p−qmCt(pm−t−qm−t)
p−qmCt(pt+qt)
p−qmCt(pm−t+qm−t)
The coefficient of αt is p−qmCt(pm−t−qm−t).
Solution
The given expression is a sum of m terms: S=(α+p)m−1+(α+p)m−2(α+q)+(α+p)m−3(α+q)2+......+(α+q)m−1
This is a geometric progression (GP) with:
- First term (A): A=(α+p)m−1
- Common ratio (R): R=(α+p)m−1(α+p)m−2(α+q)=α+pα+q
- Number of terms (N): The powers of (α+p) range from (m−1) down to 0, and powers of (α+q) range from 0 up to (m−1). This indicates there are m terms. So, N=m.
Since p=q, it implies that R=α+pα+q=1. Therefore, we can use the formula for the sum of a finite GP: SN=1−RA(1−RN).
Substitute the values of A, R, and N into the formula: S=1−α+pα+q(α+p)m−1(1−(α+pα+q)m)
Simplify the numerator: Numerator =(α+p)m−1(1−(α+p)m(α+q)m) =(α+p)m−1((α+p)m(α+p)m−(α+q)m) =(α+p)(α+p)m−(α+q)m
Simplify the denominator: Denominator =1−α+pα+q =α+p(α+p)−(α+q) =α+pp−q
Now, divide the simplified numerator by the simplified denominator: S=α+pp−qα+p(α+p)m−(α+q)m S=p−q(α+p)m−(α+q)m
To find the coefficient of αt in this expression, we use the binomial theorem for (α+p)m and (α+q)m: (α+p)m=∑k=0mmCkαkpm−k (α+q)m=∑k=0mmCkαkqm−k
Substitute these expansions back into the expression for S: S=p−q1(∑k=0mmCkαkpm−k−∑k=0mmCkαkqm−k) S=p−q1∑k=0mmCkαk(pm−k−qm−k)
To find the coefficient of αt, we set k=t in the summation: Coefficient of αt=p−q1mCt(pm−t−qm−t)
Comparing this with the given options, it matches option (B).
