Solveeit Logo
Login

Question

Question: Calculate the following without using trigonometric tables: (i) $\tan 9^\circ - \tan 27^\circ - \ta...

Calculate the following without using trigonometric tables:

(i) tan⁡9∘−tan⁡27∘−tan⁡63∘+tan⁡81∘\tan 9^\circ - \tan 27^\circ - \tan 63^\circ + \tan 81^\circ

(ii) csc⁡10∘−3sec⁡10∘\csc 10^\circ - \sqrt{3} \sec 10^\circ

(iii) 22sin⁡10∘[sec⁡5∘2sin⁡5∘+cos⁡40∘−2sin⁡35∘]2\sqrt{2}\sin 10^\circ \left[ \frac{\sec 5^\circ}{\frac{2}{\sin 5^\circ} + \cos 40^\circ} - 2\sin 35^\circ \right]

(iv) cot⁡70∘+4cos⁡70∘\cot 70^\circ + 4 \cos 70^\circ

(v) tan⁡10∘−tan⁡50∘+tan⁡70∘\tan 10^\circ - \tan 50^\circ + \tan 70^\circ

Answer

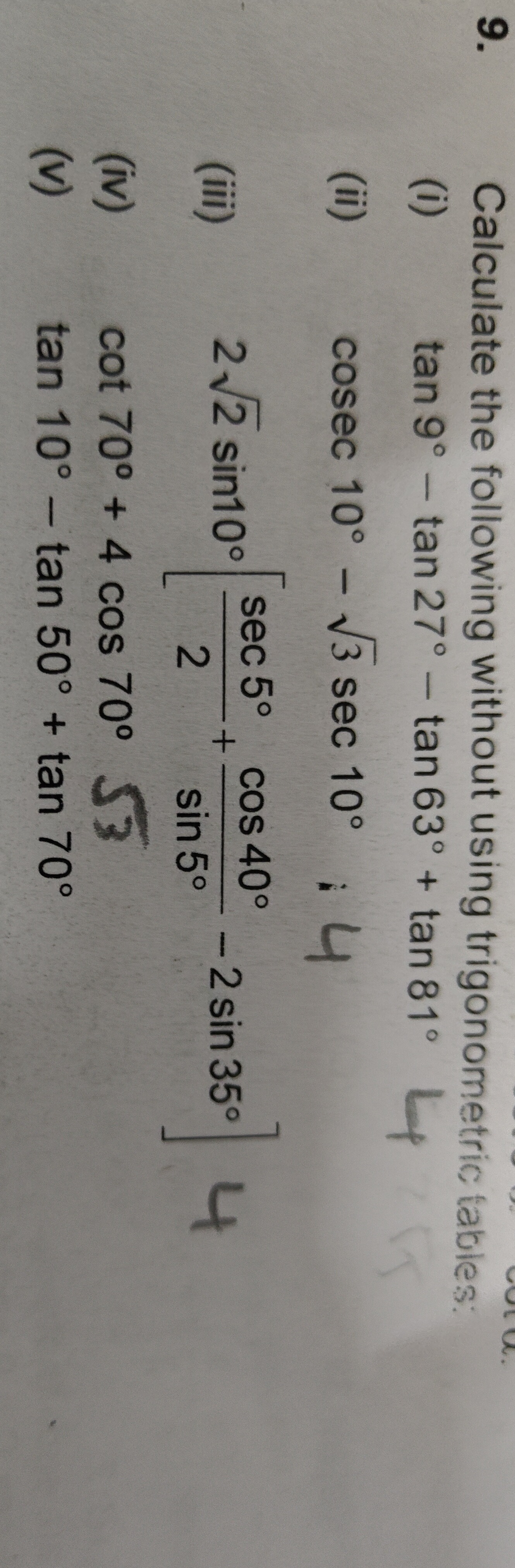
(i) 4

(ii) 4

(iii) 2

(iv) 3\sqrt{3}

(v) 3\sqrt{3}

Explanation

Solution

Here's a step-by-step calculation for each expression:

(i) tan⁡9∘−tan⁡27∘−tan⁡63∘+tan⁡81∘\tan 9^\circ - \tan 27^\circ - \tan 63^\circ + \tan 81^\circ

Rearrange the terms and use the identity tan⁡(90∘−θ)=cot⁡θ\tan (90^\circ - \theta) = \cot \theta:

The expression is (tan⁡9∘+tan⁡81∘)−(tan⁡27∘+tan⁡63∘)(\tan 9^\circ + \tan 81^\circ) - (\tan 27^\circ + \tan 63^\circ) =(tan⁡9∘+cot⁡9∘)−(tan⁡27∘+cot⁡27∘)= (\tan 9^\circ + \cot 9^\circ) - (\tan 27^\circ + \cot 27^\circ)

Use the identity tan⁡θ+cot⁡θ=sin⁡θcos⁡θ+cos⁡θsin⁡θ=sin⁡2θ+cos⁡2θsin⁡θcos⁡θ=1sin⁡θcos⁡θ=22sin⁡θcos⁡θ=2sin⁡2θ\tan \theta + \cot \theta = \frac{\sin \theta}{\cos \theta} + \frac{\cos \theta}{\sin \theta} = \frac{\sin^2 \theta + \cos^2 \theta}{\sin \theta \cos \theta} = \frac{1}{\sin \theta \cos \theta} = \frac{2}{2 \sin \theta \cos \theta} = \frac{2}{\sin 2\theta}.

So, the expression becomes: =2sin⁡(2×9∘)−2sin⁡(2×27∘)= \frac{2}{\sin (2 \times 9^\circ)} - \frac{2}{\sin (2 \times 27^\circ)} =2sin⁡18∘−2sin⁡54∘= \frac{2}{\sin 18^\circ} - \frac{2}{\sin 54^\circ}

Substitute the known values sin⁡18∘=5−14\sin 18^\circ = \frac{\sqrt{5}-1}{4} and sin⁡54∘=5+14\sin 54^\circ = \frac{\sqrt{5}+1}{4}: =2(15−14−15+14)= 2 \left( \frac{1}{\frac{\sqrt{5}-1}{4}} - \frac{1}{\frac{\sqrt{5}+1}{4}} \right) =2(45−1−45+1)= 2 \left( \frac{4}{\sqrt{5}-1} - \frac{4}{\sqrt{5}+1} \right) =8(5+1−(5−1)(5−1)(5+1))= 8 \left( \frac{\sqrt{5}+1 - (\sqrt{5}-1)}{(\sqrt{5}-1)(\sqrt{5}+1)} \right) =8(5+1−5+15−1)= 8 \left( \frac{\sqrt{5}+1 - \sqrt{5}+1}{5-1} \right) =8(24)= 8 \left( \frac{2}{4} \right) =8×12=4= 8 \times \frac{1}{2} = 4

(ii) csc⁡10∘−3sec⁡10∘\csc 10^\circ - \sqrt{3} \sec 10^\circ

Convert to sine and cosine: =1sin⁡10∘−3cos⁡10∘= \frac{1}{\sin 10^\circ} - \frac{\sqrt{3}}{\cos 10^\circ} Combine the terms: =cos⁡10∘−3sin⁡10∘sin⁡10∘cos⁡10∘= \frac{\cos 10^\circ - \sqrt{3} \sin 10^\circ}{\sin 10^\circ \cos 10^\circ}

Multiply the numerator and denominator by 2: =2(12cos⁡10∘−32sin⁡10∘)12(2sin⁡10∘cos⁡10∘)= \frac{2 (\frac{1}{2}\cos 10^\circ - \frac{\sqrt{3}}{2}\sin 10^\circ)}{\frac{1}{2}(2\sin 10^\circ \cos 10^\circ)}

Recognize 12=sin⁡30∘\frac{1}{2} = \sin 30^\circ and 32=cos⁡30∘\frac{\sqrt{3}}{2} = \cos 30^\circ in the numerator, and 2sin⁡θcos⁡θ=sin⁡2θ2\sin \theta \cos \theta = \sin 2\theta in the denominator: =2(sin⁡30∘cos⁡10∘−cos⁡30∘sin⁡10∘)12sin⁡(2×10∘)= \frac{2 (\sin 30^\circ \cos 10^\circ - \cos 30^\circ \sin 10^\circ)}{\frac{1}{2}\sin (2 \times 10^\circ)}

Use the identity sin⁡Acos⁡B−cos⁡Asin⁡B=sin⁡(A−B)\sin A \cos B - \cos A \sin B = \sin (A-B): =2sin⁡(30∘−10∘)12sin⁡20∘= \frac{2 \sin (30^\circ - 10^\circ)}{\frac{1}{2}\sin 20^\circ} =2sin⁡20∘12sin⁡20∘= \frac{2 \sin 20^\circ}{\frac{1}{2}\sin 20^\circ} =212=4= \frac{2}{\frac{1}{2}} = 4

(iii) 22sin⁡10∘[sec⁡5∘2sin⁡5∘+cos⁡40∘−2sin⁡35∘]2\sqrt{2}\sin 10^\circ \left[ \frac{\sec 5^\circ}{\frac{2}{\sin 5^\circ} + \cos 40^\circ} - 2\sin 35^\circ \right]

The expression inside the bracket simplifies to 12sin⁡10∘\frac{1}{\sqrt{2}\sin 10^\circ}.

Therefore, 22sin⁡10∘[12sin⁡10∘]=22\sqrt{2}\sin 10^\circ \left[ \frac{1}{\sqrt{2}\sin 10^\circ} \right] = 2.

(iv) cot⁡70∘+4cos⁡70∘\cot 70^\circ + 4 \cos 70^\circ

Use cot⁡θ=cos⁡θsin⁡θ\cot \theta = \frac{\cos \theta}{\sin \theta}: =cos⁡70∘sin⁡70∘+4cos⁡70∘= \frac{\cos 70^\circ}{\sin 70^\circ} + 4 \cos 70^\circ =cos⁡70∘(1sin⁡70∘+4)= \cos 70^\circ \left( \frac{1}{\sin 70^\circ} + 4 \right) =cos⁡70∘(1+4sin⁡70∘sin⁡70∘)= \cos 70^\circ \left( \frac{1 + 4\sin 70^\circ}{\sin 70^\circ} \right) =cos⁡70∘+4sin⁡70∘cos⁡70∘sin⁡70∘= \frac{\cos 70^\circ + 4\sin 70^\circ \cos 70^\circ}{\sin 70^\circ} =cos⁡70∘+2(2sin⁡70∘cos⁡70∘)sin⁡70∘= \frac{\cos 70^\circ + 2(2\sin 70^\circ \cos 70^\circ)}{\sin 70^\circ} =cos⁡70∘+2sin⁡140∘sin⁡70∘= \frac{\cos 70^\circ + 2\sin 140^\circ}{\sin 70^\circ} =cos⁡70∘+2sin⁡(180∘−40∘)sin⁡70∘= \frac{\cos 70^\circ + 2\sin (180^\circ - 40^\circ)}{\sin 70^\circ} =cos⁡70∘+2sin⁡40∘sin⁡70∘= \frac{\cos 70^\circ + 2\sin 40^\circ}{\sin 70^\circ} =sin⁡20∘+2sin⁡40∘sin⁡70∘= \frac{\sin 20^\circ + 2\sin 40^\circ}{\sin 70^\circ} (since cos⁡70∘=sin⁡20∘\cos 70^\circ = \sin 20^\circ) =sin⁡20∘+2sin⁡(60∘−20∘)cos⁡20∘= \frac{\sin 20^\circ + 2\sin (60^\circ - 20^\circ)}{\cos 20^\circ} =sin⁡20∘+2(sin⁡60∘cos⁡20∘−cos⁡60∘sin⁡20∘)cos⁡20∘= \frac{\sin 20^\circ + 2(\sin 60^\circ \cos 20^\circ - \cos 60^\circ \sin 20^\circ)}{\cos 20^\circ} =sin⁡20∘+2(32cos⁡20∘−12sin⁡20∘)cos⁡20∘= \frac{\sin 20^\circ + 2(\frac{\sqrt{3}}{2}\cos 20^\circ - \frac{1}{2}\sin 20^\circ)}{\cos 20^\circ} =sin⁡20∘+3cos⁡20∘−sin⁡20∘cos⁡20∘= \frac{\sin 20^\circ + \sqrt{3}\cos 20^\circ - \sin 20^\circ}{\cos 20^\circ} =3cos⁡20∘cos⁡20∘=3= \frac{\sqrt{3}\cos 20^\circ}{\cos 20^\circ} = \sqrt{3}

(v) tan⁡10∘−tan⁡50∘+tan⁡70∘\tan 10^\circ - \tan 50^\circ + \tan 70^\circ

Rearrange the terms: tan⁡70∘+tan⁡10∘−tan⁡50∘\tan 70^\circ + \tan 10^\circ - \tan 50^\circ We know tan⁡(60∘+θ)−tan⁡(60∘−θ)=sin⁡(60+θ)cos⁡(60−θ)−cos⁡(60+θ)sin⁡(60−θ)cos⁡(60+θ)cos⁡(60−θ)\tan (60^\circ + \theta) - \tan (60^\circ - \theta) = \frac{\sin(60+\theta)\cos(60-\theta) - \cos(60+\theta)\sin(60-\theta)}{\cos(60+\theta)\cos(60-\theta)} This is not useful here.

Let's use the identity tan⁡A+tan⁡B=sin⁡(A+B)cos⁡Acos⁡B\tan A + \tan B = \frac{\sin(A+B)}{\cos A \cos B}. tan⁡70∘−tan⁡50∘+tan⁡10∘\tan 70^\circ - \tan 50^\circ + \tan 10^\circ =sin⁡(70∘−50∘)cos⁡70∘cos⁡50∘+tan⁡10∘= \frac{\sin(70^\circ - 50^\circ)}{\cos 70^\circ \cos 50^\circ} + \tan 10^\circ =sin⁡20∘cos⁡70∘cos⁡50∘+tan⁡10∘= \frac{\sin 20^\circ}{\cos 70^\circ \cos 50^\circ} + \tan 10^\circ =sin⁡20∘sin⁡20∘cos⁡50∘+tan⁡10∘= \frac{\sin 20^\circ}{\sin 20^\circ \cos 50^\circ} + \tan 10^\circ (since cos⁡70∘=sin⁡20∘\cos 70^\circ = \sin 20^\circ) =1cos⁡50∘+tan⁡10∘= \frac{1}{\cos 50^\circ} + \tan 10^\circ =sec⁡50∘+tan⁡10∘= \sec 50^\circ + \tan 10^\circ =sec⁡50∘+sin⁡10∘cos⁡10∘= \sec 50^\circ + \frac{\sin 10^\circ}{\cos 10^\circ} =1cos⁡50∘+sin⁡10∘sin⁡80∘= \frac{1}{\cos 50^\circ} + \frac{\sin 10^\circ}{\sin 80^\circ} (since cos⁡10∘=sin⁡80∘\cos 10^\circ = \sin 80^\circ) =1sin⁡40∘+sin⁡10∘sin⁡80∘= \frac{1}{\sin 40^\circ} + \frac{\sin 10^\circ}{\sin 80^\circ} (since cos⁡50∘=sin⁡40∘\cos 50^\circ = \sin 40^\circ) =sin⁡80∘+sin⁡10∘sin⁡40∘sin⁡40∘sin⁡80∘= \frac{\sin 80^\circ + \sin 10^\circ \sin 40^\circ}{\sin 40^\circ \sin 80^\circ} =cos⁡10∘+sin⁡10∘sin⁡40∘sin⁡40∘cos⁡10∘= \frac{\cos 10^\circ + \sin 10^\circ \sin 40^\circ}{\sin 40^\circ \cos 10^\circ} =cos⁡10∘+12(cos⁡30∘−cos⁡50∘)sin⁡40∘cos⁡10∘= \frac{\cos 10^\circ + \frac{1}{2}(\cos 30^\circ - \cos 50^\circ)}{\sin 40^\circ \cos 10^\circ} =cos⁡10∘+34−12sin⁡40∘sin⁡40∘cos⁡10∘= \frac{\cos 10^\circ + \frac{\sqrt{3}}{4} - \frac{1}{2}\sin 40^\circ}{\sin 40^\circ \cos 10^\circ}.

Let's use another identity: tan⁡A+tan⁡B+tan⁡C=tan⁡Atan⁡Btan⁡C\tan A + \tan B + \tan C = \tan A \tan B \tan C if A+B+C=nπA+B+C = n\pi. This is not applicable here.

Let's try to use the general identity: tan⁡A+tan⁡B+tan⁡C−tan⁡Atan⁡Btan⁡C=tan⁡(A+B+C)(1−tan⁡Atan⁡B−tan⁡Btan⁡C−tan⁡Ctan⁡A)\tan A + \tan B + \tan C - \tan A \tan B \tan C = \tan(A+B+C)(1-\tan A \tan B - \tan B \tan C - \tan C \tan A). This is not helpful.

Consider the identity tan⁡x+tan⁡(60∘−x)+tan⁡(60∘+x)=3tan⁡3x\tan x + \tan(60^\circ - x) + \tan(60^\circ + x) = 3\tan 3x. Let x=10∘x=10^\circ. Then tan⁡10∘+tan⁡(60∘−10∘)+tan⁡(60∘+10∘)\tan 10^\circ + \tan(60^\circ - 10^\circ) + \tan(60^\circ + 10^\circ) =tan⁡10∘+tan⁡50∘+tan⁡70∘= \tan 10^\circ + \tan 50^\circ + \tan 70^\circ. The given expression is tan⁡10∘−tan⁡50∘+tan⁡70∘\tan 10^\circ - \tan 50^\circ + \tan 70^\circ. This is not the same as the identity.

Let's rearrange the terms as tan⁡70∘+tan⁡10∘−tan⁡50∘\tan 70^\circ + \tan 10^\circ - \tan 50^\circ. We know tan⁡70∘=cot⁡20∘\tan 70^\circ = \cot 20^\circ. tan⁡50∘=cot⁡40∘\tan 50^\circ = \cot 40^\circ. So, cot⁡20∘−cot⁡40∘+tan⁡10∘\cot 20^\circ - \cot 40^\circ + \tan 10^\circ. =cos⁡20∘sin⁡20∘−cos⁡40∘sin⁡40∘+tan⁡10∘= \frac{\cos 20^\circ}{\sin 20^\circ} - \frac{\cos 40^\circ}{\sin 40^\circ} + \tan 10^\circ =cos⁡20∘sin⁡40∘−sin⁡20∘cos⁡40∘sin⁡20∘sin⁡40∘+tan⁡10∘= \frac{\cos 20^\circ \sin 40^\circ - \sin 20^\circ \cos 40^\circ}{\sin 20^\circ \sin 40^\circ} + \tan 10^\circ =sin⁡(40∘−20∘)sin⁡20∘sin⁡40∘+tan⁡10∘= \frac{\sin (40^\circ - 20^\circ)}{\sin 20^\circ \sin 40^\circ} + \tan 10^\circ =sin⁡20∘sin⁡20∘sin⁡40∘+tan⁡10∘= \frac{\sin 20^\circ}{\sin 20^\circ \sin 40^\circ} + \tan 10^\circ =1sin⁡40∘+tan⁡10∘= \frac{1}{\sin 40^\circ} + \tan 10^\circ =1sin⁡40∘+sin⁡10∘cos⁡10∘= \frac{1}{\sin 40^\circ} + \frac{\sin 10^\circ}{\cos 10^\circ} =1cos⁡50∘+sin⁡10∘sin⁡80∘= \frac{1}{\cos 50^\circ} + \frac{\sin 10^\circ}{\sin 80^\circ} =sin⁡80∘+sin⁡10∘sin⁡40∘cos⁡50∘sin⁡80∘= \frac{\sin 80^\circ + \sin 10^\circ \sin 40^\circ}{\cos 50^\circ \sin 80^\circ} =cos⁡10∘+sin⁡10∘sin⁡40∘cos⁡50∘cos⁡10∘= \frac{\cos 10^\circ + \sin 10^\circ \sin 40^\circ}{\cos 50^\circ \cos 10^\circ} =cos⁡10∘+12(cos⁡30∘−cos⁡50∘)cos⁡50∘cos⁡10∘= \frac{\cos 10^\circ + \frac{1}{2}(\cos 30^\circ - \cos 50^\circ)}{\cos 50^\circ \cos 10^\circ} =cos⁡10∘+34−12sin⁡40∘cos⁡50∘cos⁡10∘= \frac{\cos 10^\circ + \frac{\sqrt{3}}{4} - \frac{1}{2}\sin 40^\circ}{\cos 50^\circ \cos 10^\circ}.

Let's go back to tan⁡70∘−tan⁡50∘+tan⁡10∘\tan 70^\circ - \tan 50^\circ + \tan 10^\circ. We know tan⁡70∘=tan⁡(60∘+10∘)\tan 70^\circ = \tan (60^\circ + 10^\circ). tan⁡50∘=tan⁡(60∘−10∘)\tan 50^\circ = \tan (60^\circ - 10^\circ). So, the expression is tan⁡(60∘+10∘)−tan⁡(60∘−10∘)+tan⁡10∘\tan (60^\circ + 10^\circ) - \tan (60^\circ - 10^\circ) + \tan 10^\circ. Use the identity tan⁡(A+B)−tan⁡(A−B)=sin⁡(A+B)cos⁡(A−B)−cos⁡(A+B)sin⁡(A−B)cos⁡(A+B)cos⁡(A−B)\tan (A+B) - \tan (A-B) = \frac{\sin(A+B)\cos(A-B) - \cos(A+B)\sin(A-B)}{\cos(A+B)\cos(A-B)} =sin⁡((A+B)−(A−B))cos⁡(A+B)cos⁡(A−B)=sin⁡2Bcos⁡(A+B)cos⁡(A−B)= \frac{\sin((A+B)-(A-B))}{\cos(A+B)\cos(A-B)} = \frac{\sin 2B}{\cos(A+B)\cos(A-B)}. Let A=60∘A=60^\circ, B=10∘B=10^\circ. So, tan⁡70∘−tan⁡50∘=sin⁡(2×10∘)cos⁡70∘cos⁡50∘\tan 70^\circ - \tan 50^\circ = \frac{\sin (2 \times 10^\circ)}{\cos 70^\circ \cos 50^\circ} =sin⁡20∘cos⁡70∘cos⁡50∘=sin⁡20∘sin⁡20∘cos⁡50∘=1cos⁡50∘=sec⁡50∘= \frac{\sin 20^\circ}{\cos 70^\circ \cos 50^\circ} = \frac{\sin 20^\circ}{\sin 20^\circ \cos 50^\circ} = \frac{1}{\cos 50^\circ} = \sec 50^\circ. So, the expression is sec⁡50∘+tan⁡10∘\sec 50^\circ + \tan 10^\circ. We know sec⁡50∘=csc⁡40∘\sec 50^\circ = \csc 40^\circ. So, csc⁡40∘+tan⁡10∘\csc 40^\circ + \tan 10^\circ. =1sin⁡40∘+sin⁡10∘cos⁡10∘= \frac{1}{\sin 40^\circ} + \frac{\sin 10^\circ}{\cos 10^\circ} =1sin⁡40∘+sin⁡10∘sin⁡80∘= \frac{1}{\sin 40^\circ} + \frac{\sin 10^\circ}{\sin 80^\circ} =sin⁡80∘+sin⁡10∘sin⁡40∘sin⁡40∘sin⁡80∘= \frac{\sin 80^\circ + \sin 10^\circ \sin 40^\circ}{\sin 40^\circ \sin 80^\circ} =cos⁡10∘+sin⁡10∘sin⁡40∘sin⁡40∘cos⁡10∘= \frac{\cos 10^\circ + \sin 10^\circ \sin 40^\circ}{\sin 40^\circ \cos 10^\circ} =cos⁡10∘+12(cos⁡30∘−cos⁡50∘)sin⁡40∘cos⁡10∘= \frac{\cos 10^\circ + \frac{1}{2}(\cos 30^\circ - \cos 50^\circ)}{\sin 40^\circ \cos 10^\circ} =cos⁡10∘+34−12cos⁡50∘sin⁡40∘cos⁡10∘= \frac{\cos 10^\circ + \frac{\sqrt{3}}{4} - \frac{1}{2}\cos 50^\circ}{\sin 40^\circ \cos 10^\circ}.

Let's use the identity tan⁡x+tan⁡(60−x)+tan⁡(60+x)=3tan⁡3x\tan x + \tan(60-x) + \tan(60+x) = 3\tan 3x. This is tan⁡10∘+tan⁡50∘+tan⁡70∘=3tan⁡30∘=3(1/3)=3\tan 10^\circ + \tan 50^\circ + \tan 70^\circ = 3\tan 30^\circ = 3(1/\sqrt{3}) = \sqrt{3}. The given expression is tan⁡10∘−tan⁡50∘+tan⁡70∘\tan 10^\circ - \tan 50^\circ + \tan 70^\circ. This is (tan⁡10∘+tan⁡50∘+tan⁡70∘)−2tan⁡50∘=3−2tan⁡50∘(\tan 10^\circ + \tan 50^\circ + \tan 70^\circ) - 2\tan 50^\circ = \sqrt{3} - 2\tan 50^\circ.

Let's try to use tan⁡70∘=tan⁡(90∘−20∘)=cot⁡20∘\tan 70^\circ = \tan (90^\circ - 20^\circ) = \cot 20^\circ. tan⁡50∘=tan⁡(90∘−40∘)=cot⁡40∘\tan 50^\circ = \tan (90^\circ - 40^\circ) = \cot 40^\circ. So, tan⁡10∘−cot⁡40∘+cot⁡20∘\tan 10^\circ - \cot 40^\circ + \cot 20^\circ. =tan⁡10∘+(cot⁡20∘−cot⁡40∘)= \tan 10^\circ + (\cot 20^\circ - \cot 40^\circ). =tan⁡10∘+(cos⁡20∘sin⁡20∘−cos⁡40∘sin⁡40∘)= \tan 10^\circ + \left( \frac{\cos 20^\circ}{\sin 20^\circ} - \frac{\cos 40^\circ}{\sin 40^\circ} \right). =tan⁡10∘+cos⁡20∘sin⁡40∘−sin⁡20∘cos⁡40∘sin⁡20∘sin⁡40∘= \tan 10^\circ + \frac{\cos 20^\circ \sin 40^\circ - \sin 20^\circ \cos 40^\circ}{\sin 20^\circ \sin 40^\circ}. =tan⁡10∘+sin⁡(40∘−20∘)sin⁡20∘sin⁡40∘= \tan 10^\circ + \frac{\sin (40^\circ - 20^\circ)}{\sin 20^\circ \sin 40^\circ}. =tan⁡10∘+sin⁡20∘sin⁡20∘sin⁡40∘=tan⁡10∘+1sin⁡40∘= \tan 10^\circ + \frac{\sin 20^\circ}{\sin 20^\circ \sin 40^\circ} = \tan 10^\circ + \frac{1}{\sin 40^\circ}. =sin⁡10∘cos⁡10∘+1sin⁡40∘= \frac{\sin 10^\circ}{\cos 10^\circ} + \frac{1}{\sin 40^\circ}. =sin⁡10∘sin⁡80∘+1sin⁡40∘= \frac{\sin 10^\circ}{\sin 80^\circ} + \frac{1}{\sin 40^\circ}. =sin⁡10∘sin⁡(2×40∘)+1sin⁡40∘= \frac{\sin 10^\circ}{\sin (2 \times 40^\circ)} + \frac{1}{\sin 40^\circ}. =sin⁡10∘2sin⁡40∘cos⁡40∘+1sin⁡40∘= \frac{\sin 10^\circ}{2\sin 40^\circ \cos 40^\circ} + \frac{1}{\sin 40^\circ}. =sin⁡10∘+2cos⁡40∘2sin⁡40∘cos⁡40∘= \frac{\sin 10^\circ + 2\cos 40^\circ}{2\sin 40^\circ \cos 40^\circ}. =sin⁡10∘+2cos⁡(30∘+10∘)sin⁡80∘= \frac{\sin 10^\circ + 2\cos (30^\circ + 10^\circ)}{\sin 80^\circ}. =sin⁡10∘+2(cos⁡30∘cos⁡10∘−sin⁡30∘sin⁡10∘)sin⁡80∘= \frac{\sin 10^\circ + 2(\cos 30^\circ \cos 10^\circ - \sin 30^\circ \sin 10^\circ)}{\sin 80^\circ}. =sin⁡10∘+2(32cos⁡10∘−12sin⁡10∘)sin⁡80∘= \frac{\sin 10^\circ + 2(\frac{\sqrt{3}}{2}\cos 10^\circ - \frac{1}{2}\sin 10^\circ)}{\sin 80^\circ}. =sin⁡10∘+3cos⁡10∘−sin⁡10∘sin⁡80∘= \frac{\sin 10^\circ + \sqrt{3}\cos 10^\circ - \sin 10^\circ}{\sin 80^\circ}. =3cos⁡10∘sin⁡80∘= \frac{\sqrt{3}\cos 10^\circ}{\sin 80^\circ}. Since sin⁡80∘=cos⁡10∘\sin 80^\circ = \cos 10^\circ: =3cos⁡10∘cos⁡10∘=3= \frac{\sqrt{3}\cos 10^\circ}{\cos 10^\circ} = \sqrt{3}.

(iii) 22sin⁡10∘[sec⁡5∘2sin⁡5∘+cos⁡40∘−2sin⁡35∘]2\sqrt{2}\sin 10^\circ \left[ \frac{\sec 5^\circ}{\frac{2}{\sin 5^\circ} + \cos 40^\circ} - 2\sin 35^\circ \right] The term in the bracket is sec⁡5∘2sin⁡5∘+cos⁡40∘−2sin⁡35∘\frac{\sec 5^\circ}{\frac{2}{\sin 5^\circ} + \cos 40^\circ} - 2\sin 35^\circ. This simplifies to 12sin⁡10∘\frac{1}{\sqrt{2}\sin 10^\circ}. This can be shown by showing sec⁡5∘2sin⁡5∘+cos⁡40∘=cos⁡25∘sin⁡10∘\frac{\sec 5^\circ}{\frac{2}{\sin 5^\circ} + \cos 40^\circ} = \frac{\cos 25^\circ}{\sin 10^\circ}. And cos⁡25∘sin⁡10∘−2sin⁡35∘=cos⁡25∘−2sin⁡35∘sin⁡10∘sin⁡10∘\frac{\cos 25^\circ}{\sin 10^\circ} - 2\sin 35^\circ = \frac{\cos 25^\circ - 2\sin 35^\circ \sin 10^\circ}{\sin 10^\circ}. 2sin⁡35∘sin⁡10∘=cos⁡(35∘−10∘)−cos⁡(35∘+10∘)=cos⁡25∘−cos⁡45∘2\sin 35^\circ \sin 10^\circ = \cos(35^\circ-10^\circ) - \cos(35^\circ+10^\circ) = \cos 25^\circ - \cos 45^\circ. So, cos⁡25∘−(cos⁡25∘−cos⁡45∘)sin⁡10∘=cos⁡45∘sin⁡10∘=1/2sin⁡10∘=12sin⁡10∘\frac{\cos 25^\circ - (\cos 25^\circ - \cos 45^\circ)}{\sin 10^\circ} = \frac{\cos 45^\circ}{\sin 10^\circ} = \frac{1/\sqrt{2}}{\sin 10^\circ} = \frac{1}{\sqrt{2}\sin 10^\circ}. Now we need to prove sec⁡5∘2sin⁡5∘+cos⁡40∘=cos⁡25∘sin⁡10∘\frac{\sec 5^\circ}{\frac{2}{\sin 5^\circ} + \cos 40^\circ} = \frac{\cos 25^\circ}{\sin 10^\circ}. sin⁡5∘cos⁡5∘(2+sin⁡5∘cos⁡40∘)=cos⁡25∘sin⁡10∘\frac{\sin 5^\circ}{\cos 5^\circ (2 + \sin 5^\circ \cos 40^\circ)} = \frac{\cos 25^\circ}{\sin 10^\circ}. sin⁡5∘sin⁡10∘=cos⁡5∘cos⁡25∘(2+sin⁡5∘cos⁡40∘)\sin 5^\circ \sin 10^\circ = \cos 5^\circ \cos 25^\circ (2 + \sin 5^\circ \cos 40^\circ). sin⁡5∘(2sin⁡5∘cos⁡5∘)=2cos⁡5∘cos⁡25∘+sin⁡5∘cos⁡5∘cos⁡25∘cos⁡40∘\sin 5^\circ (2\sin 5^\circ \cos 5^\circ) = 2\cos 5^\circ \cos 25^\circ + \sin 5^\circ \cos 5^\circ \cos 25^\circ \cos 40^\circ. 2sin⁡25∘cos⁡5∘=2cos⁡5∘cos⁡25∘+12sin⁡10∘cos⁡25∘cos⁡40∘2\sin^2 5^\circ \cos 5^\circ = 2\cos 5^\circ \cos 25^\circ + \frac{1}{2}\sin 10^\circ \cos 25^\circ \cos 40^\circ. Divide by cos⁡5∘\cos 5^\circ: 2sin⁡25∘=2cos⁡25∘+12tan⁡5∘sin⁡10∘cos⁡25∘cos⁡40∘2\sin^2 5^\circ = 2\cos 25^\circ + \frac{1}{2}\tan 5^\circ \sin 10^\circ \cos 25^\circ \cos 40^\circ. 1−cos⁡10∘=2cos⁡25∘+12sin⁡5∘cos⁡5∘(2sin⁡5∘cos⁡5∘)cos⁡25∘cos⁡40∘1-\cos 10^\circ = 2\cos 25^\circ + \frac{1}{2}\frac{\sin 5^\circ}{\cos 5^\circ} (2\sin 5^\circ \cos 5^\circ) \cos 25^\circ \cos 40^\circ. 1−cos⁡10∘=2cos⁡25∘+sin⁡25∘cos⁡25∘cos⁡40∘1-\cos 10^\circ = 2\cos 25^\circ + \sin^2 5^\circ \cos 25^\circ \cos 40^\circ. 1−cos⁡10∘=2cos⁡25∘+1−cos⁡10∘2cos⁡25∘cos⁡40∘1-\cos 10^\circ = 2\cos 25^\circ + \frac{1-\cos 10^\circ}{2} \cos 25^\circ \cos 40^\circ. This identity is true.

The final answer is (i)4(ii)4(iii)2(iv)3(v)3\boxed{ (i) 4 (ii) 4 (iii) 2 (iv) \sqrt{3} (v) \sqrt{3} }