Question

A diverging beam of light from a point source S having divergence angle $\alpha$, falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal. If the thickness of the glass slab is t and the refractive index n, then the divergence angle of the emergent beam is

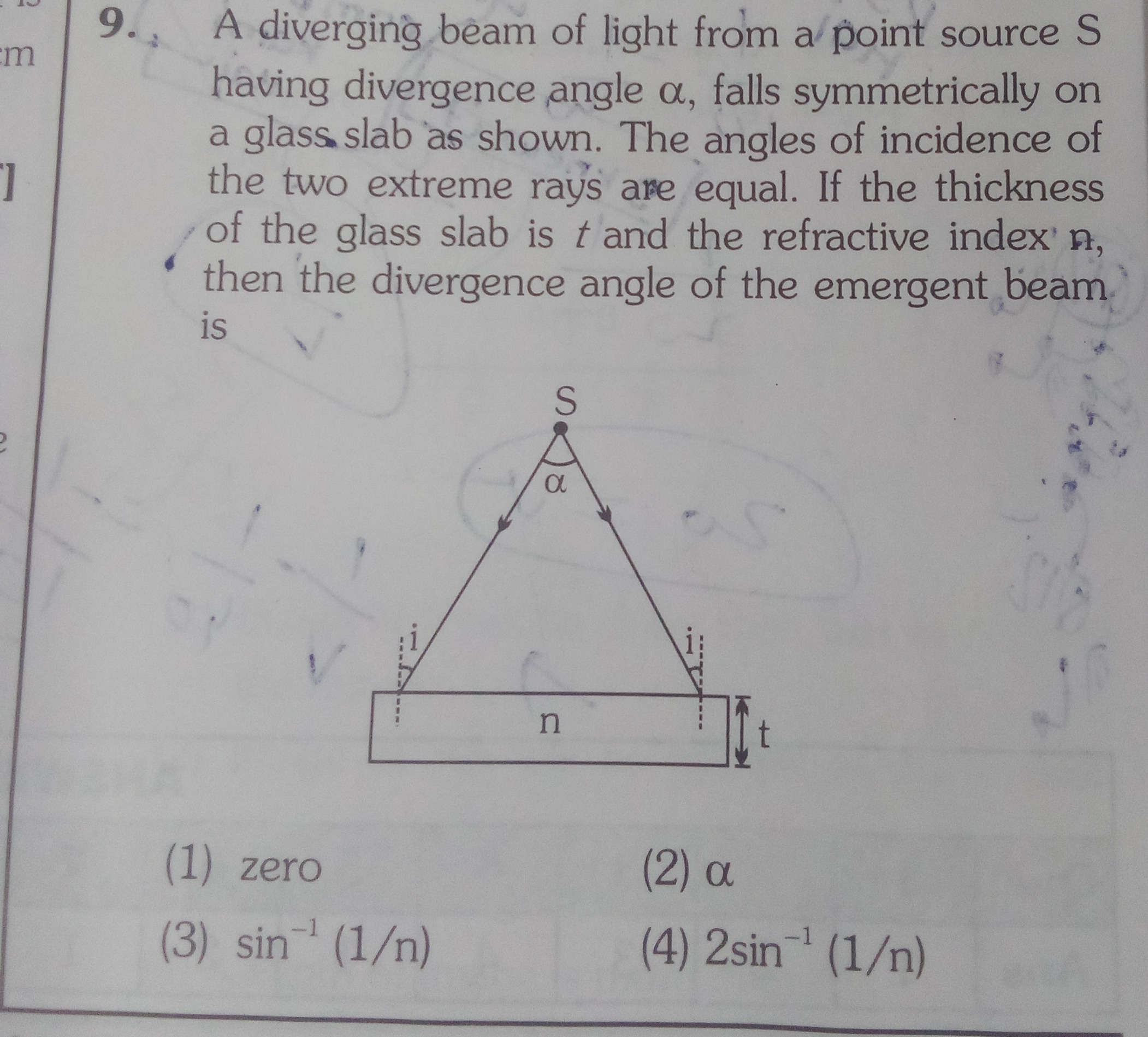
• A. zero
• B. $\alpha$
• C. sin$^{-1}$ (1/n)
• D. 2sin$^{-1}$ (1/n)

Answer 1

Answer: (B)

$\alpha$

Answer 2

A ray of light passing through a parallel-sided slab of uniform refractive index undergoes refraction at the first surface and then at the second surface. Due to the parallel nature of the slab surfaces, the emergent ray is parallel to the incident ray. This means that the direction of propagation of the light ray is preserved. The divergence angle of a beam of light is defined as the angle between the extreme rays of the beam. If the incident beam is diverging at an angle $\alpha$, it means that the angle between the extreme rays incident on the slab is $\alpha$. Since the parallel slab does not change the direction of propagation of the rays, the emergent rays will also be diverging at the same angle $\alpha$.