Question

If a, b ∈ [0, 2π] and the equation x² + 4 + 3 sin(ax + b) - 2x = 0 has at least one solution, then the value of (a + b) can be

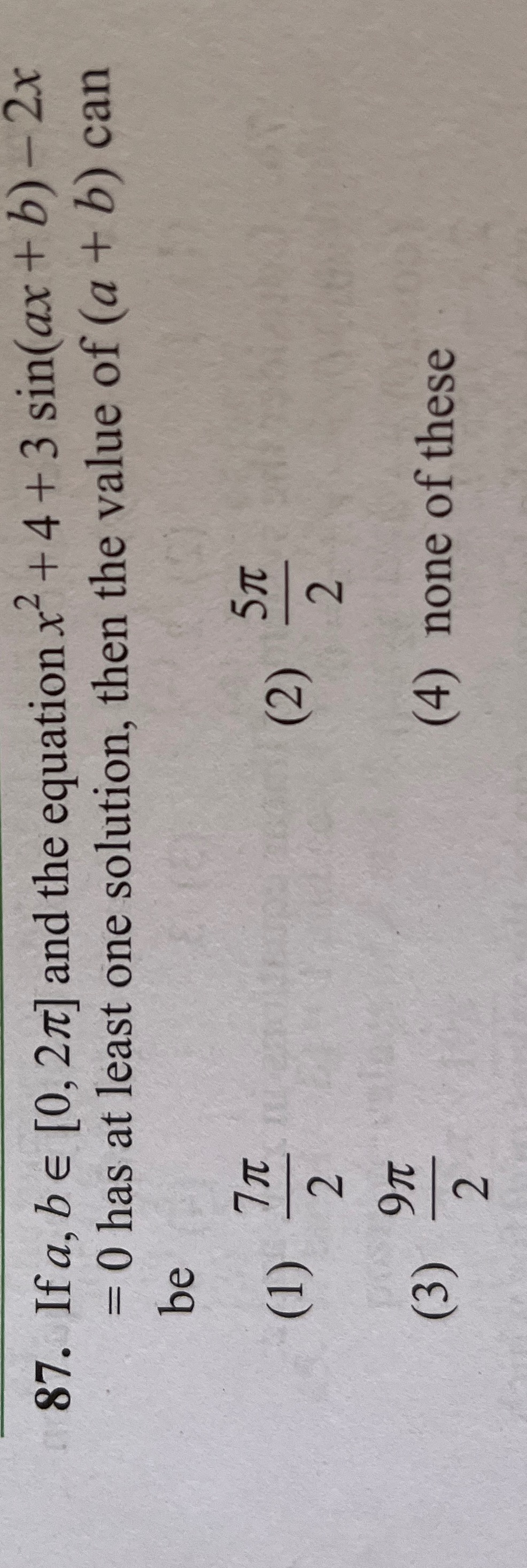
• A. $\frac{7\pi}{2}$
• B. $\frac{5\pi}{2}$
• C. $\frac{9\pi}{2}$
• D. none of these

Answer 1

Answer: (A)

$\frac{7\pi}{2}$

Answer 2

Given

$$x^2 + 4 + 3\sin(ax+b) - 2x = 0,$$

rewrite the quadratic part by completing the square:

$$x^2 - 2x + 4 = (x-1)^2 + 3.$$

Thus,

$$(x-1)^2 + 3 + 3\sin(ax+b) = 0 \quad \Rightarrow \quad (x-1)^2 + 3(1+\sin(ax+b)) = 0.$$

Since $(x-1)^2 \ge 0$ and $1+\sin(ax+b) \ge 0$ (because $\sin(ax+b) \ge -1$), the sum can be zero only if both terms are zero. Therefore, we require:

$$(x-1)^2 = 0 \quad \text{and} \quad 1+\sin(ax+b)=0.$$

The first condition gives:

$$x = 1.$$

The second condition gives:

$$\sin(ax+b) = -1.$$

At $x=1$, this becomes:

$$\sin(a\cdot 1 + b) = \sin(a+b) = -1.$$

This equation is satisfied when:

$$a+b = \frac{3\pi}{2} + 2\pi k,\quad k\in \mathbb{Z}.$$

Since $a,\,b\in [0,2\pi]$, their sum lies in $[0,4\pi]$. The possible sums in this interval are:

$$\frac{3\pi}{2} \quad (\text{for } k=0) \quad \text{and} \quad \frac{7\pi}{2} \quad (\text{for } k=1).$$

Among the provided options, only option (1) $\frac{7\pi}{2}$ is valid (note that $\frac{3\pi}{2}$ is not listed, and the other options do not produce $\sin(a+b)=-1$).