Question

Let $A = \begin{bmatrix} 1 & -1 & 1 \\ 2 & 1 & -3 \\ 1 & 1 & 1 \end{bmatrix}$ and $B = \begin{bmatrix} 4 \\ 0 \\ 2 \end{bmatrix}$ such that $AX = B$, then $X =$

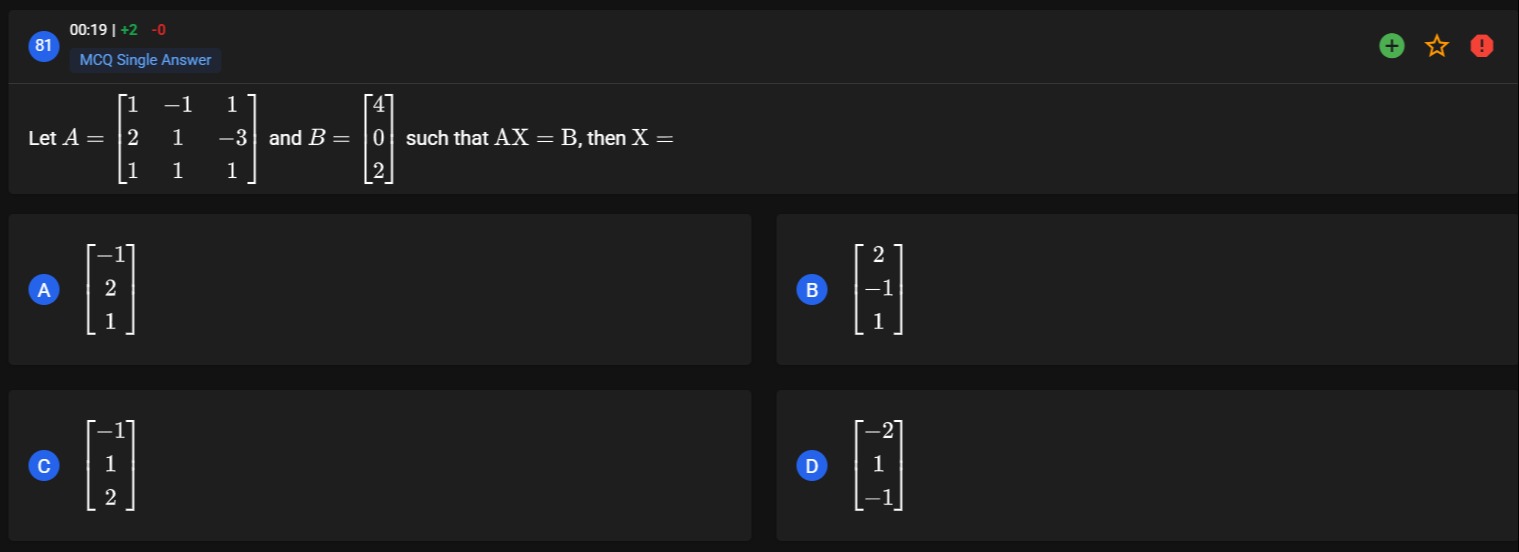
• A. $\begin{bmatrix} -1 \\ 2 \\ 1 \end{bmatrix}$
• B. $\begin{bmatrix} 2 \\ -1 \\ 1 \end{bmatrix}$
• C. $\begin{bmatrix} -1 \\ 1 \\ 2 \end{bmatrix}$
• D. $\begin{bmatrix} -2 \\ 1 \\ -1 \end{bmatrix}$

Answer 1

Answer: (B)

$\begin{bmatrix} 2 \\ -1 \\ 1 \end{bmatrix}$

Answer 2

1. Extract equations from $AX = B$.

2. Subtract eq. (1) from (3) to find $y=-1$.

3. Substitute $y$ into eq. (1) to get $x+z=3$.

4. Substitute $y$ into eq. (2) and use $x = 3-z$ to solve for $z$.

5. Find $x$ from $x+z=3$.