Question

A convex lens of focal length f is placed somewhere between an object and a screen. The distance between the object and the screen is x. If the magnification is m, the focal length of the lens is given by:

• A. $\frac{mx}{(m+1)^2}$
• B. $\frac{(m-1)^2 x}{m}$
• C. $\frac{mx}{(m-1)^2}$
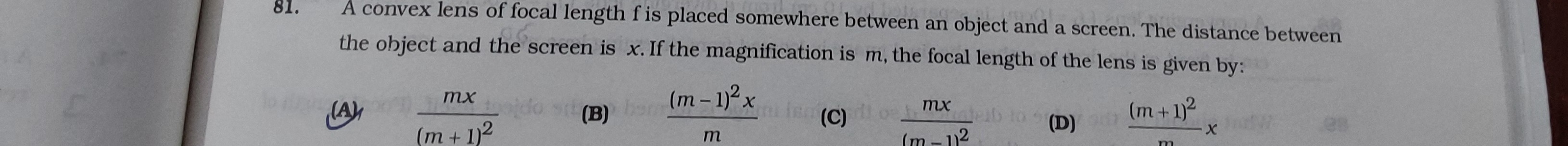
• D. $\frac{(m+1)^2}{m}x$

Answer 1

Answer: (A)

$\frac{mx}{(m+1)^2}$

Answer 2

To determine the focal length of the convex lens, we use the lens formula and the magnification formula, along with the given distance between the object and the screen.

Let:

• $u$ be the object distance from the lens.
• $v$ be the image distance from the lens.
• $f$ be the focal length of the lens.
• $x$ be the distance between the object and the screen.
• $m$ be the numerical value (magnitude) of the magnification.

1. Sign Convention:

For a real object placed to the left of the lens, $u$ is negative. For a real image formed on a screen by a convex lens, $v$ is positive.

2. Distance between Object and Screen ($x$):

Since the image is real and formed on a screen, the object and image are on opposite sides of the lens. Therefore, the distance between the object and the screen is the sum of the magnitudes of the object and image distances:

$x = |u| + |v|$

Using sign convention, $x = -u + v$ (since $u$ is negative, $-u$ is positive).

3. Magnification ($m$):

The magnification $M$ is given by $M = \frac{v}{u}$. For a real image formed by a convex lens, the image is inverted, so the magnification $M$ is negative. If $m$ is the numerical value (magnitude) of magnification, then $M = -m$.

So, $\frac{v}{u} = -m$

This implies $v = -mu$.

4. Express $u$ and $v$ in terms of $x$ and $m$:

Substitute $v = -mu$ into the distance equation:

$x = -u + (-mu)$

$x = -u(1+m)$

From this, we can find $u$:

$u = -\frac{x}{1+m}$

Now, substitute the value of $u$ back into the equation for $v$:

$v = -m \left(-\frac{x}{1+m}\right)$

$v = \frac{mx}{1+m}$

5. Apply the Lens Formula:

The lens formula is $\frac{1}{f} = \frac{1}{v} - \frac{1}{u}$.

Substitute the expressions for $u$ and $v$:

$\frac{1}{f} = \frac{1}{\left(\frac{mx}{1+m}\right)} - \frac{1}{\left(-\frac{x}{1+m}\right)}$

$\frac{1}{f} = \frac{1+m}{mx} + \frac{1+m}{x}$

To combine the terms on the right side, find a common denominator, which is $mx$:

$\frac{1}{f} = \frac{1+m}{mx} + \frac{m(1+m)}{mx}$

$\frac{1}{f} = \frac{(1+m) + m(1+m)}{mx}$

Factor out $(1+m)$ from the numerator:

$\frac{1}{f} = \frac{(1+m)(1+m)}{mx}$

$\frac{1}{f} = \frac{(1+m)^2}{mx}$

6. Solve for $f$:

Inverting both sides gives the focal length $f$:

$f = \frac{mx}{(1+m)^2}$

Comparing this result with the given options, the derived focal length matches option (A).