Question

If $P(\theta) = \begin{bmatrix} 1 & cot\theta \\ -cot\theta & 1 \end{bmatrix}$ and $\underline{PQ=I}$, then

$(cosec^2\theta)Q$ is given by:

(where $I$ is an identity matrix of $2 \times 2$ order)

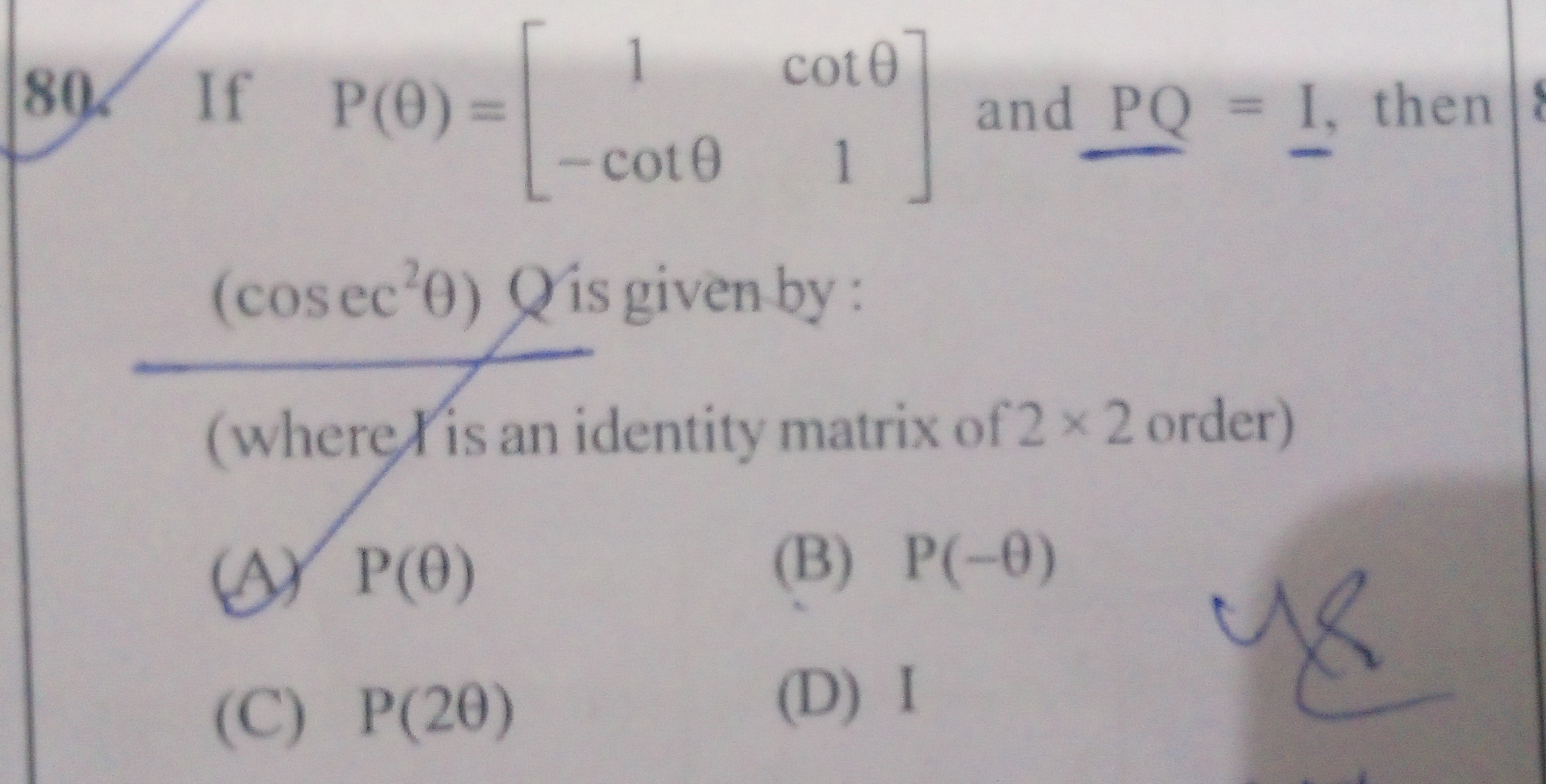
• A. $P(\theta)$
• B. $P(-\theta)$
• C. $P(2\theta)$
• D. $I$

Answer 1

Answer: (B)

$P(-\theta)$

Answer 2

Given

$$P(\theta)=\begin{bmatrix}1 & \cot\theta\\ -\cot\theta & 1\end{bmatrix},$$

and $PQ=I$ so that $Q=P^{-1}$.

Step 1: Find $\det(P(\theta))$:

$$\det(P(\theta))=1\cdot1 - (-\cot\theta)(\cot\theta)=1+\cot^2\theta=\csc^2\theta.$$

Step 2: Find the inverse:

$$P^{-1}=\frac{1}{\csc^2\theta}\begin{bmatrix}1 & -\cot\theta\\ \cot\theta & 1\end{bmatrix}.$$

Thus,

$$Q=P^{-1}=\frac{1}{\csc^2\theta}\begin{bmatrix}1 & -\cot\theta\\ \cot\theta & 1\end{bmatrix}.$$

Step 3: Multiply by $\csc^2\theta$:

$$\csc^2\theta\, Q = \begin{bmatrix} 1 & -\cot\theta \\ \cot\theta & 1 \end{bmatrix}.$$

Step 4: Compare with $P(-\theta)$:

$$P(-\theta)=\begin{bmatrix}1 & \cot(-\theta)\\ -\cot(-\theta) & 1\end{bmatrix}=\begin{bmatrix}1 & -\cot\theta\\ \cot\theta & 1\end{bmatrix}.$$

Thus,

$$\csc^2\theta\, Q = P(-\theta).$$