Question

A block of mass m is released from rest. Initially the spring is unstretched. The pulley and strings are ideal. The maximum energy stored in the spring is

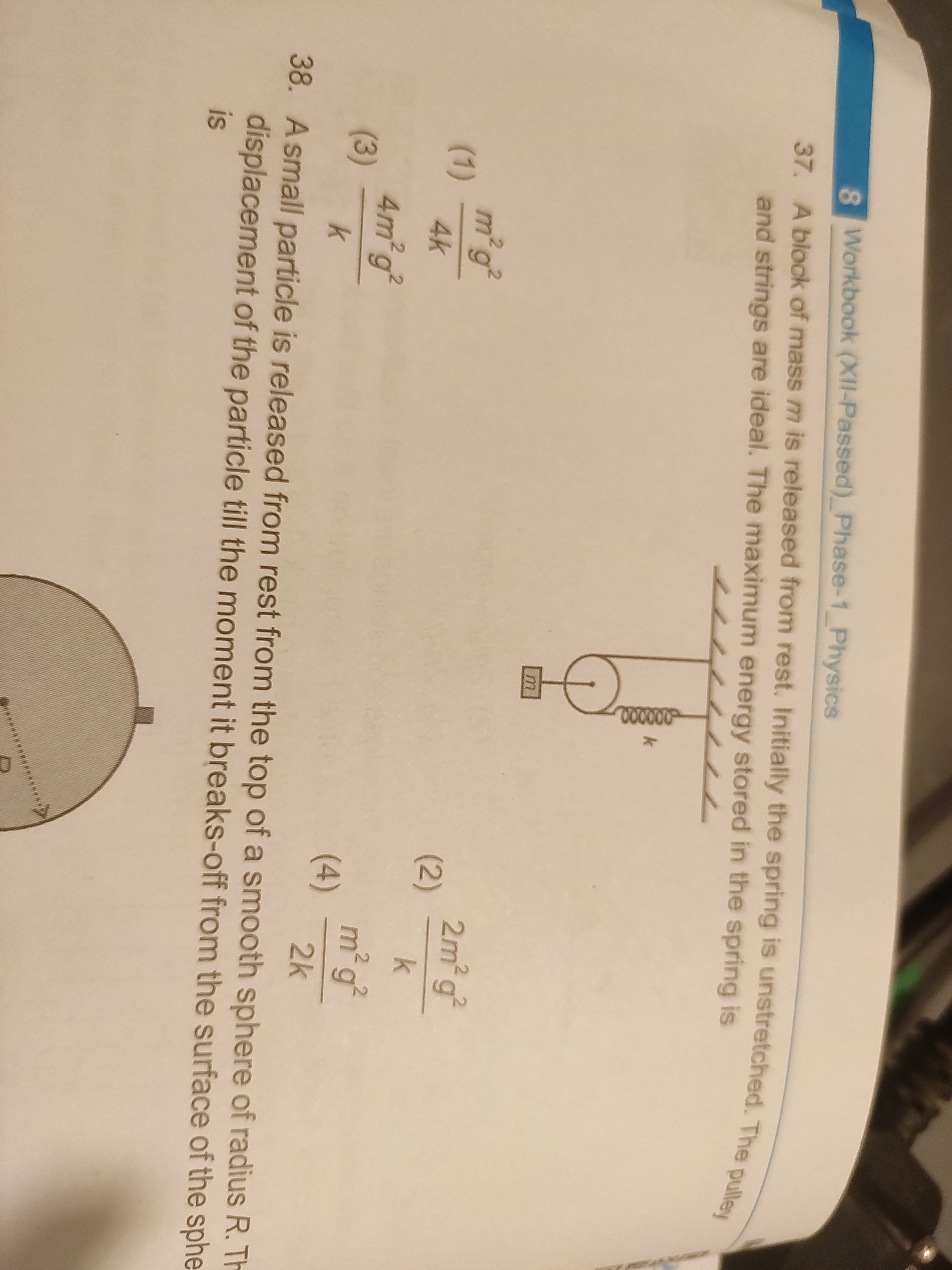
• A. $\frac{m^2g^2}{4k}$
• B. $\frac{2m^2 g^2}{k}$
• C. $\frac{4m^2g^2}{k}$
• D. $\frac{m^2 g^2}{2k}$

Answer 1

Answer: (B)

$\frac{2m^2g^2}{k}$

Answer 2

The maximum energy in the spring occurs at maximum extension ($x_{max}$), where the block's velocity is momentarily zero. Using conservation of mechanical energy:

Initial Energy (KE=0, PE_g=0, PE_s=0) = Final Energy (KE=0, PE_g=-mg$x_{max}$, PE_s=$\frac{1}{2}kx_{max}^2$)

$0 = -mgx_{max} + \frac{1}{2}kx_{max}^2$

$mgx_{max} = \frac{1}{2}kx_{max}^2 \implies x_{max} = \frac{2mg}{k}$

Maximum energy stored in spring = $\frac{1}{2}kx_{max}^2 = \frac{1}{2}k\left(\frac{2mg}{k}\right)^2 = \frac{2m^2g^2}{k}$.