Solveeit Logo
Login

Question

Question: Three vectors $\vec{A}$, $\vec{B}$ and $\vec{C}$ each of magnitude 10 units are shown in figure. Fin...

Three vectors A⃗\vec{A}, B⃗\vec{B} and C⃗\vec{C} each of magnitude 10 units are shown in figure. Find resultant vector :

A

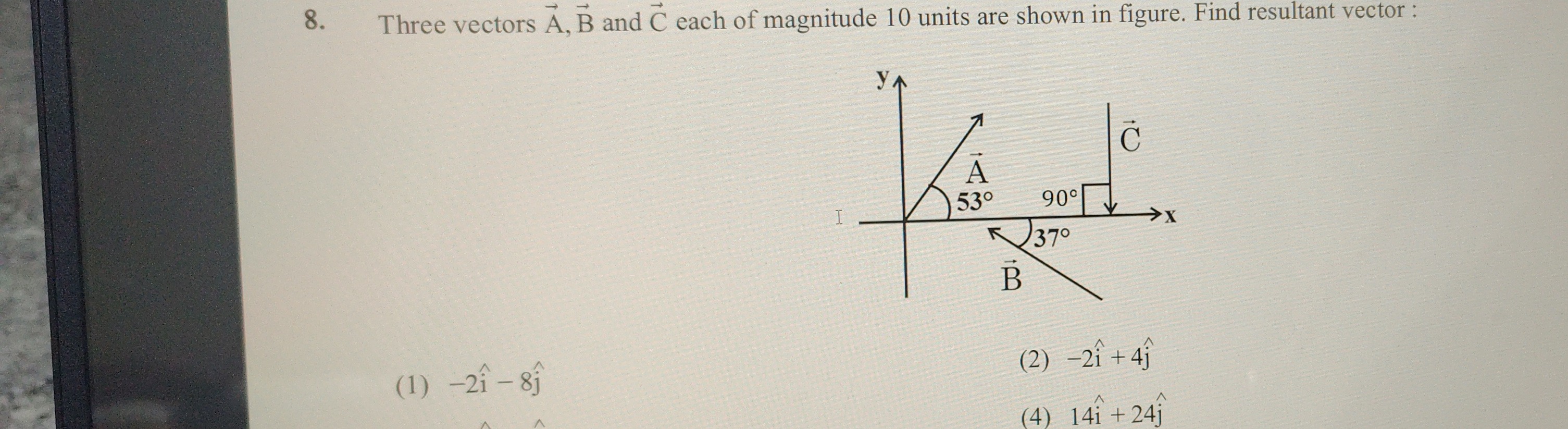
-2\hat{i}-8\hat{j}

B

-2\hat{i}+4\hat{j}

C

14\hat{i}+24\hat{j}

Answer

-2\hat{i}-8\hat{j}

Explanation

Solution

To find the resultant vector, we need to express each vector in its component form (i^\hat{i} and j^\hat{j}) and then sum them up. The magnitude of each vector is given as 10 units. We will use the common approximations for trigonometric values: sin⁡(37∘)=3/5\sin(37^\circ) = 3/5, cos⁡(37∘)=4/5\cos(37^\circ) = 4/5, sin⁡(53∘)=4/5\sin(53^\circ) = 4/5, cos⁡(53∘)=3/5\cos(53^\circ) = 3/5.

  1. Vector A⃗\vec{A}:

    • Magnitude ∣A⃗∣=10|\vec{A}| = 10 units.
    • Direction: 53∘53^\circ with the positive x-axis in the first quadrant.
    • X-component: Ax=∣A⃗∣cos⁡(53∘)=10×(3/5)=6A_x = |\vec{A}| \cos(53^\circ) = 10 \times (3/5) = 6
    • Y-component: Ay=∣A⃗∣sin⁡(53∘)=10×(4/5)=8A_y = |\vec{A}| \sin(53^\circ) = 10 \times (4/5) = 8
    • So, A⃗=6i^+8j^\vec{A} = 6\hat{i} + 8\hat{j}

  2. Vector B⃗\vec{B}:

    • Magnitude ∣B⃗∣=10|\vec{B}| = 10 units.

    • Direction: Assuming the angle 37∘37^\circ is with the negative x-axis in the third quadrant (to match the option), B⃗=−10cos⁡(37∘)i^−10sin⁡(37∘)j^=−8i^−6j^\vec{B} = -10 \cos(37^\circ)\hat{i} - 10 \sin(37^\circ)\hat{j} = -8\hat{i} - 6\hat{j}.

    • X-component: Bx=−∣B⃗∣cos⁡(37∘)=−10×(4/5)=−8B_x = -|\vec{B}| \cos(37^\circ) = -10 \times (4/5) = -8

    • Y-component: By=−∣B⃗∣sin⁡(37∘)=−10×(3/5)=−6B_y = -|\vec{B}| \sin(37^\circ) = -10 \times (3/5) = -6

    • So, B⃗=−8i^−6j^\vec{B} = -8\hat{i} - 6\hat{j}

  3. Vector C⃗\vec{C}:

    • Magnitude ∣C⃗∣=10|\vec{C}| = 10 units.
    • Direction: The vector is pointing vertically downwards along the negative y-axis.
    • X-component: Cx=0C_x = 0
    • Y-component: Cy=−∣C⃗∣=−10C_y = -|\vec{C}| = -10
    • So, C⃗=0i^−10j^\vec{C} = 0\hat{i} - 10\hat{j}

  4. Resultant Vector R⃗\vec{R}: The resultant vector is the sum of the individual vectors: R⃗=A⃗+B⃗+C⃗\vec{R} = \vec{A} + \vec{B} + \vec{C}.

    • X-component of R⃗\vec{R}: Rx=Ax+Bx+Cx=6+(−8)+0=−2R_x = A_x + B_x + C_x = 6 + (-8) + 0 = -2

    • Y-component of R⃗\vec{R}: Ry=Ay+By+Cy=8+(−6)+(−10)=8−6−10=−8R_y = A_y + B_y + C_y = 8 + (-6) + (-10) = 8 - 6 - 10 = -8

    • Therefore, the resultant vector is R⃗=−2i^−8j^\vec{R} = -2\hat{i} - 8\hat{j}.

The resultant vector is −2i^−8j^-2\hat{i}-8\hat{j}. The correct option is (1).