Question
Question: The magnetic moment of the arrangement shown in the figure is ...
The magnetic moment of the arrangement shown in the figure is
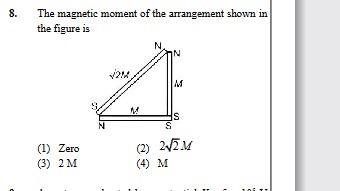
Zero
22M
2 M
M
2 M
Solution
The magnetic moment of a bar magnet is a vector quantity directed from its South pole to its North pole. Its magnitude is given by m * L, where m is the pole strength and L is the length of the magnet.
Let's analyze the three magnets in the arrangement:
-
Horizontal Magnet:
- Its North pole is on the left and South pole is on the right.
- Its length is labeled as 'M' in the figure. Let's assume its magnetic moment has a magnitude of
M(the variable used in the options). - Since the magnetic moment vector points from S to N, for the horizontal magnet, it points to the left.
- Let's set up a coordinate system where the bottom-left corner is the origin (0,0), the horizontal direction is the x-axis, and the vertical direction is the y-axis.
- Magnetic moment vector of horizontal magnet: M1=−Mi^
-
Vertical Magnet:
- Its South pole is at the bottom and North pole is at the top.
- Its length is labeled as 'M' in the figure. So, its magnetic moment has a magnitude of
M. - The magnetic moment vector points from S to N, so it points upwards.
- Magnetic moment vector of vertical magnet: M2=Mj^
-
Hypotenuse Magnet:
- Its South pole is at the bottom-left and North pole is at the top-right.
- Its length is labeled as
$\sqrt{2}M$in the figure. If we assume the magnetic moment is proportional to length (i.e., pole strength 'm' is constant for all magnets), then its magnetic moment magnitude is 2M. - The triangle is a right-angled isosceles triangle (sides M and M), so the hypotenuse makes an angle of 45 degrees with the horizontal and vertical axes.
- The magnetic moment vector points from S to N, i.e., along the hypotenuse from bottom-left to top-right.
- We can resolve this vector into its x and y components:
- x-component: (2M)cos45∘=(2M)21=M
- y-component: (2M)sin45∘=(2M)21=M
- Magnetic moment vector of hypotenuse magnet: M3=Mi^+Mj^
Net Magnetic Moment:
The total magnetic moment of the arrangement is the vector sum of the individual magnetic moments: Mnet=M1+M2+M3 Mnet=(−Mi^)+(Mj^)+(Mi^+Mj^)
Combine the i^ components: (−M+M)i^=0i^ Combine the j^ components: (M+M)j^=2Mj^
So, Mnet=0i^+2Mj^=2Mj^
The magnitude of the net magnetic moment is ∣Mnet∣=(0)2+(2M)2=4M2=2M.
The final answer is 2 M.
Explanation of the solution:
- Identify the direction of the magnetic moment for each bar magnet (from South to North pole).
- Assign magnitudes to each magnetic moment based on the given labels (M, M, 2M).
- Represent each magnetic moment as a vector using a coordinate system.
- Horizontal magnet: M1=−Mi^
- Vertical magnet: M2=Mj^
- Hypotenuse magnet: M3=Mi^+Mj^ (resolved into components as it's at 45 degrees).
- Calculate the net magnetic moment by vector addition: Mnet=M1+M2+M3.
- Sum the components: Mnet=(−M+M)i^+(M+M)j^=2Mj^.
- The magnitude of the net magnetic moment is ∣2Mj^∣=2M.
The final answer is 2 M. The correct option is (3).
