Question

The figure shows the velocity and acceleration of a point like body at the initial moment of its motion. The acceleration vector of the body remains constant. The minimum radius of curvature of trajectory of the body is:

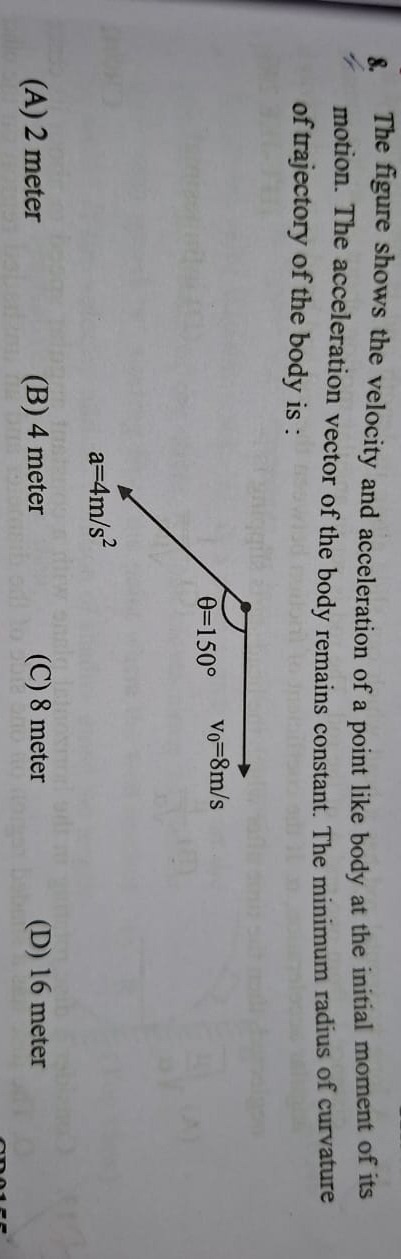
• A. 2 meter
• B. 4 meter
• C. 8 meter
• D. 16 meter

Answer 1

Answer: (B)

4 meter

Answer 2

The radius of curvature $R$ of a trajectory is given by $R = \frac{v^2}{a_n}$, where $v$ is the speed of the body and $a_n$ is the normal component of acceleration. The velocity at time $t$ is given by $\vec{v}(t) = \vec{v}_0 + \vec{a}t$, where $\vec{v}_0$ is the initial velocity and $\vec{a}$ is the constant acceleration. The speed squared is $v(t)^2 = |\vec{v}_0 + \vec{a}t|^2 = v_0^2 + 2(\vec{v}_0 \cdot \vec{a})t + a^2t^2$. The minimum speed occurs when $\frac{d(v^2)}{dt} = 0$, which yields $t = -\frac{\vec{v}_0 \cdot \vec{a}}{a^2}$. Given $\theta = 150^\circ$ between $\vec{v}_0$ and $\vec{a}$, $\vec{v}_0 \cdot \vec{a} = v_0 a \cos 150^\circ < 0$. Thus, the time for minimum speed is positive. The minimum speed is $v_{min} = |v_0 \sin \theta|$. At the point of minimum speed, the tangential acceleration $a_t = \frac{dv}{dt} = 0$. This implies that the acceleration is purely normal, so $a_n = a$. Therefore, the minimum radius of curvature is $R_{min} = \frac{v_{min}^2}{a_n} = \frac{v_{min}^2}{a}$. Given $v_0 = 8$ m/s, $a = 4$ m/s$^2$, and $\theta = 150^\circ$: $v_{min} = |8 \sin 150^\circ| = |8 \times \frac{1}{2}| = 4$ m/s. $R_{min} = \frac{(4 \text{ m/s})^2}{4 \text{ m/s}^2} = \frac{16 \text{ m}^2/\text{s}^2}{4 \text{ m/s}^2} = 4$ meters.