Question

The equations of two waves are gives as $y_1 = a \sin(\omega t + \phi_1)$, $y_2 = a \sin(\omega t + \phi_2)$. If amplitude and time period of resultant wave is same as the individual waves. Then $(\phi_1 - \phi_2)$ is

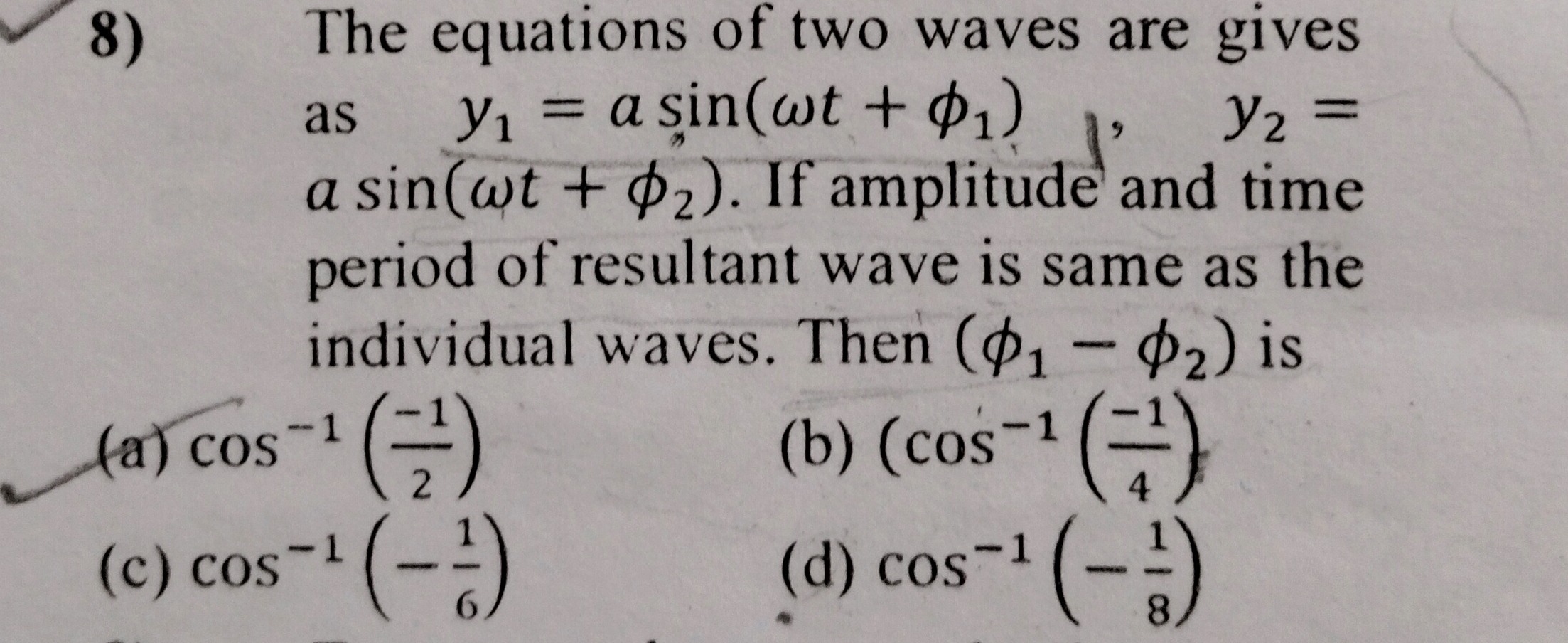
• A. $\cos^{-1}(-\frac{1}{2})$
• B. $(\cos^{-1}(-\frac{1}{4})$
• C. $\cos^{-1}(-\frac{1}{6})$
• D. $\cos^{-1}(-\frac{1}{8})$

Answer 1

Answer: (A)

$\cos^{-1}(-\frac{1}{2})$

Answer 2

The resultant wave from the two waves is given by:

$$y = y_1 + y_2 = a\sin(\omega t + \phi_1) + a\sin(\omega t + \phi_2)$$

Using the sine addition formula:

$$y = 2a \cos\left(\frac{\phi_1-\phi_2}{2}\right) \sin\left(\omega t + \frac{\phi_1+\phi_2}{2}\right)$$

The amplitude of the resultant wave is $2a\cos\left(\frac{\phi_1-\phi_2}{2}\right)$.

Since the given amplitude of the resultant wave is the same as that of the individual waves (i.e. $a$):

$$2a \cos\left(\frac{\phi_1-\phi_2}{2}\right) = a \implies \cos\left(\frac{\phi_1-\phi_2}{2}\right) = \frac{1}{2}$$

Thus:

$$\frac{\phi_1-\phi_2}{2} = \frac{\pi}{3} \implies \phi_1 - \phi_2 = \frac{2\pi}{3}$$

Note that $\cos^{-1}(-\frac{1}{2}) = \frac{2\pi}{3}$.

Therefore, the phase difference $(\phi_1 - \phi_2)$ is:

$$\cos^{-1}\left(-\frac{1}{2}\right)$$