Question

The entire graph of the expression y = x² + kx - x + 9 is strictly above the x-axis if and only if

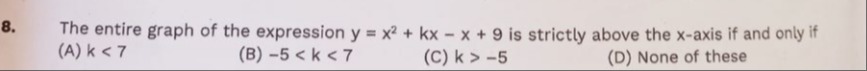
• A. k < 7
• B. -5 < k < 7
• C. k > -5
• D. None of these

Answer 1

Answer: (B)

-5 < k < 7

Answer 2

The quadratic function is

y = x^2 + kx - x + 9 = x^2 + (k-1)x + 9.

For the graph to lie strictly above the x-axis (i.e., $y > 0$ for all $x$), the quadratic must have no real roots. Since the coefficient of $x^2$ is positive, the condition is that the discriminant is negative:

\Delta = (k-1)^2 - 4(1)(9) < 0 \implies (k-1)^2 < 36.

Taking square roots:

-6 < k-1 < 6 \implies -5 < k < 7.