Question

Seawater at a frequency f = 9 × 10² Hz, has permittivity ∈ = 80∈₀ and resistivity ρ = 0.25 Ωm. Imagine a parallel plate capacitor is immersed in seawater and is driven by an alternating voltage source V(t) = V₀ sin (2πft). Then the conduction current density becomes 10ˣ times the displacement current density after time t = $\frac{1}{800}$ s. The value of x is ____ (Given: $\frac{1}{4πε₀}$ = 9×10⁹ Nm²C⁻²)

Answer 1

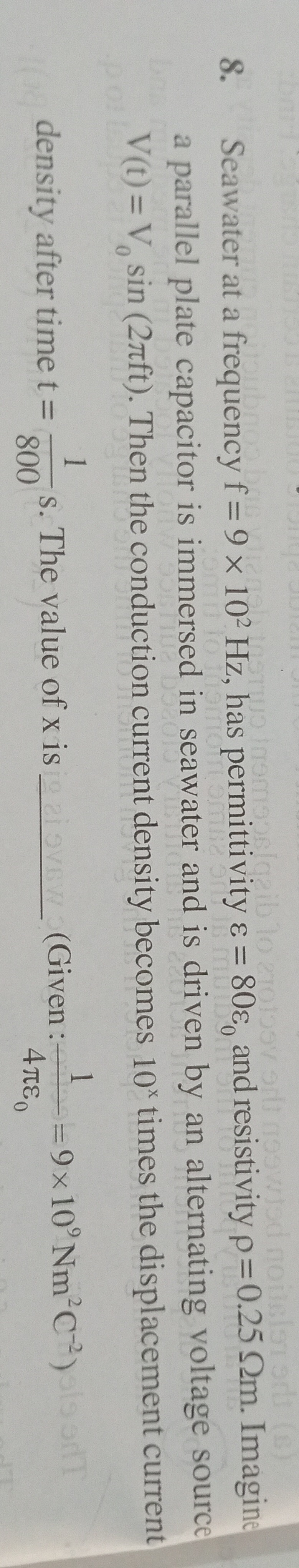
6

Answer 2

The electric field inside a parallel plate capacitor driven by an alternating voltage $V(t) = V_0 \sin(2\pi f t)$ is approximately uniform and given by $E(t) = \frac{V(t)}{d} = \frac{V_0}{d} \sin(2\pi f t)$, where $d$ is the distance between the plates.

The conduction current density is given by Ohm's law: $\vec{J}_c = \sigma \vec{E} = \frac{1}{\rho} \vec{E}$

The magnitude of the conduction current density is $|J_c(t)| = \frac{1}{\rho} |E(t)| = \frac{V_0}{\rho d} |\sin(2\pi f t)|$.

The displacement current density is given by: $\vec{J}_d = \epsilon \frac{\partial \vec{E}}{\partial t}$

$J_d(t) = \epsilon \frac{\partial}{\partial t} \left( \frac{V_0}{d} \sin(2\pi f t) \right) = \epsilon \frac{V_0}{d} (2\pi f) \cos(2\pi f t)$.

The magnitude of the displacement current density is $|J_d(t)| = \epsilon \frac{V_0}{d} (2\pi f) |\cos(2\pi f t)|$.

We are interested in the ratio of the magnitudes of the conduction current density to the displacement current density:

$\frac{|J_c(t)|}{|J_d(t)|} = \frac{\frac{V_0}{\rho d} |\sin(2\pi f t)|}{\epsilon \frac{V_0}{d} (2\pi f) |\cos(2\pi f t)|} = \frac{1}{\rho \epsilon (2\pi f)} \left| \frac{\sin(2\pi f t)}{\cos(2\pi f t)} \right| = \frac{1}{2\pi f \epsilon \rho} |\tan(2\pi f t)|$.

We are given:

• Frequency $f = 9 \times 10^2$ Hz
• Permittivity $\epsilon = 80 \epsilon_0$
• Resistivity $\rho = 0.25 \, \Omega m$
• Time $t = \frac{1}{800}$ s
• The relation $\frac{1}{4\pi \epsilon_0} = 9 \times 10^9 \, Nm^2C^{-2}$ gives $\epsilon_0 = \frac{1}{4\pi \times 9 \times 10^9} = \frac{1}{36\pi \times 10^9} \, F/m$.

Let's calculate the term $2\pi f \epsilon \rho$: $2\pi f \epsilon \rho = 2\pi (9 \times 10^2) (80 \epsilon_0) (0.25)$ $= 2\pi (900) (80 \times \frac{1}{36\pi \times 10^9}) (0.25)$ $= 1800\pi \times \frac{80}{36\pi \times 10^9} \times 0.25$ $= \frac{1800 \times 80 \times 0.25}{36 \times 10^9} = \frac{1800 \times 20}{36 \times 10^9} = \frac{36000}{36 \times 10^9} = \frac{1000}{10^9} = 10^{-6}$.

Now, let's evaluate the argument of the tangent function at $t = \frac{1}{800}$ s: $2\pi f t = 2\pi (9 \times 10^2) \left( \frac{1}{800} \right) = 2\pi \frac{900}{800} = 2\pi \frac{9}{8} = \frac{9\pi}{4}$.

The ratio of the current densities is: $\frac{|J_c(t)|}{|J_d(t)|} = \frac{1}{10^{-6}} \left| \tan\left(\frac{9\pi}{4}\right) \right|$.

We know that $\tan\left(\frac{9\pi}{4}\right) = \tan\left(2\pi + \frac{\pi}{4}\right) = \tan\left(\frac{\pi}{4}\right) = 1$. So, $\left| \tan\left(\frac{9\pi}{4}\right) \right| = |1| = 1$.

The ratio is $\frac{|J_c(t)|}{|J_d(t)|} = \frac{1}{10^{-6}} \times 1 = 10^6$.

We are given that the conduction current density becomes $10^x$ times the displacement current density. So, $\frac{|J_c(t)|}{|J_d(t)|} = 10^x$. $10^6 = 10^x$. Therefore, $x = 6$.

The final answer is $\boxed{6}$.

Explanation: The conduction current density is $J_c = E/\rho$ and the displacement current density is $J_d = \epsilon \partial E/\partial t$. For an alternating voltage $V(t) = V_0 \sin(\omega t)$, the electric field in a parallel plate capacitor is $E(t) = E_0 \sin(\omega t)$, where $E_0 = V_0/d$ and $\omega = 2\pi f$. $J_c(t) = \frac{E_0}{\rho} \sin(\omega t)$ $J_d(t) = \epsilon E_0 \omega \cos(\omega t)$ The ratio of magnitudes is $\frac{|J_c(t)|}{|J_d(t)|} = \frac{E_0/\rho |\sin(\omega t)|}{\epsilon E_0 \omega |\cos(\omega t)|} = \frac{1}{\omega \epsilon \rho} |\tan(\omega t)|$. Given $f = 9 \times 10^2$ Hz, $\epsilon = 80 \epsilon_0$, $\rho = 0.25 \, \Omega m$, $t = \frac{1}{800}$ s, and $\frac{1}{4\pi \epsilon_0} = 9 \times 10^9$. $\omega = 2\pi f = 2\pi \times 9 \times 10^2$. $\epsilon_0 = \frac{1}{36\pi \times 10^9}$. $\omega \epsilon \rho = (2\pi \times 9 \times 10^2) \times (80 \times \frac{1}{36\pi \times 10^9}) \times 0.25 = 10^{-6}$. $\omega t = (2\pi \times 9 \times 10^2) \times \frac{1}{800} = \frac{9\pi}{4}$. $\frac{|J_c(t)|}{|J_d(t)|} = \frac{1}{10^{-6}} |\tan(\frac{9\pi}{4})| = 10^6 \times 1 = 10^6$. Given $\frac{|J_c(t)|}{|J_d(t)|} = 10^x$, we have $10^x = 10^6$, so $x=6$.